14033: Розфарбування прямокутниками - Paint by Rectangles - USACO22FebPlatinum
Оскільки остання робота Бесі була зустрінута критикою, вона зробила нову, обравши на площині \(1≤N≤10^5\) прямокутників зі сторонами, що жодні дві з них не колінеарні. Кордони цих прямокутників визначають межі розмальованих регіонів. Будучи художницею-аванагардисткою, вона вирішила, що прямокутники складатимуть корови породи Holstein. Точніше, кожен регіон, обгороджений прямокутником, розфарбовується у білий чи чорний колір. Жодні два сусідні регіони не мають один і той самий колір. Регіон зовні всіх прямокутників розфарбований у білий колір.
Бесі просить вивести Вас одну з двох речей залежно від параметра \(T\):
Якщо \(T\)=1, виведіть загальну кількість регіонів.
Якщо \(T\)=2, виведіть кількість білих регіонів, за якими слідує кількість чорних регіонів.
Примітка: час на тест для цього завдання збільшено до 4с (в два рази більше звичайного часу на тест).
ФОРМАТ ВВЕДЕННЯ (з клавіатури / stdin):
Перший рядок містить \(N\) та \(T\).
Кожен з наступних \(N\) рядків містить описи прямокутника у вигляді (\(x_1,y_1\)),(\(x_2,y_2\)) де \(1≤x_1<x_2≤2N\) і \(1≤y_1<y_2≤2N\). (\(x_1,y_1\)) і (\(x_2,y_2\)) це лівий нижній і правий верхній кути прямокутника відповідно. Гарантується, що всі \(x_i\) формують перестановку 1…2\(N\). Аналогічна умова гарантується і всім \(y_i\).
ФОРМАТ ВИСНОВКУ (на екран / stdout):
Одне ціле, якщо \(T\)=1, інакше два цілих числа, розділених пробілом.
ПРИКЛАД ВВЕДЕННЯ:
2 1
1 1 3 3
2 2 4 4ПРИКЛАД ВИВЕДЕННЯ:
4Усього є два білі регіони та два чорні регіони, разом = 4 регіони. Кордони регіонів з'єднані, тому введення відповідає підзадачі 3.

ПРИКЛАД ВВЕДЕННЯ:
5 2
1 5 3 6
5 4 7 9
4 1 8 3
9 8 10 10
2 2 6 7ПРИКЛАД ВИВЕДЕННЯ:
4 5Кордон прямокутника праворуч-зверху не з'єднаний з іншими межами. Тому дане введення не відповідає підзадачі 4.
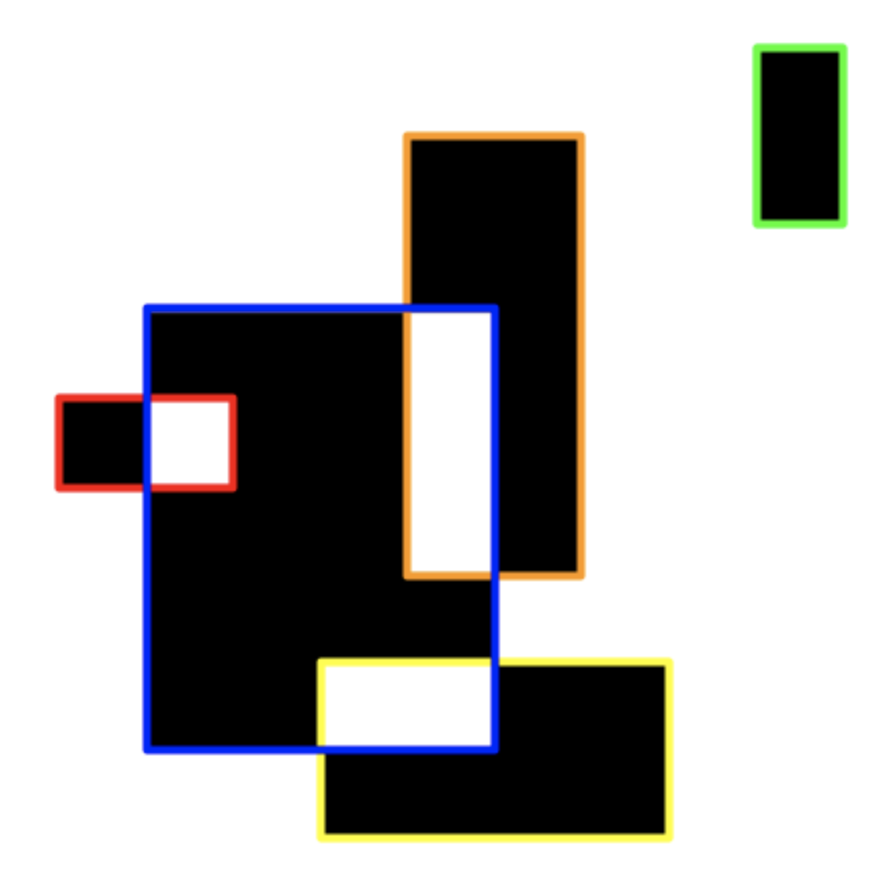
Коментарі