AVL-дерева є прикладом збалансованого бінарного дерева пошуку. У термінології AVL, підвішене бінарне дерево називається збалансованим, якщо кожної вершини висоти її лівого і правого піддерев відрізняються не більше, ніж один. Таке дерево, власне, і називається AVL-деревом. Зрозуміло, існує не єдине AVL-дерево при фіксованому числі вершин. Наприклад, існує шість AVL-дерев із п'ятьма вершинами, вони зображені на малюнку нижче.

Дерева з однаковим числом вершин можуть мати різну висоту, наприклад, на малюнку знизу намальовано два дерева з сімома вершинами, які мають висоти 2 і 3, відповідно.

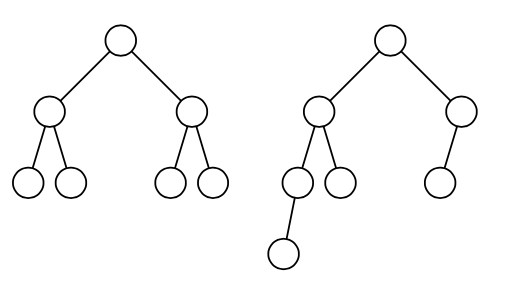
Вам дано два числа --- \(N\) і \(H\), потрібно знайти число AVL-дерев, які складаються з \(N\) вершин і мають висоту \(H\). Оскільки їх кількість досить велика, виведіть кількість за модулем \(786\,433\).

Примітка

\(786\,433\) просте число, і \(786\,433 = 3 \cdot 2^{18} + 1\).

Формат вхідних даних

Єдиний рядок вхідного файлу містить два числа --- \(N\) і \(H\) (\(1 \le N \le 65\,535\), \(0 \le H \le 15\)).

Формат вихідних даних

Виведіть однину кількість AVL дерев з \(N\) вершинами висоти \(H\), за модулем \(786\,433\).

Приклад вхідних даних

7 3

Приклад вихідних даних

16