Ви вставляєте \(N\) випадкових елементів з речовими ключами в декартове дерево. Порахуйте ймовірність того, що висота декартового дерева стане \(h\) (\(h = 0, 1, \ldots, N-1\)).

Декартове дерево - це рандомізоване бінарне дерево пошуку. Кожна вершина має свій ключ та пріоритет. У цій задачі припустимо, що обидва ці дійсні значення лежать у межах від 0 до 1.

У декартовому дереві такі умови завжди виконуються:

Умова про ключі:

• Для кожної вершини її ключ більший, ніж ключі її лівого сина і ключі нащадків її лівого сина.
• Для кожної вершини її ключ менший, ніж ключі її правого сина та ключі нащадків її правого сина.

Умова про пріоритети:

• Для кожної вершини її пріоритет більший, ніж пріоритет її дітей.

Наступна картинка показує приклад декартового дерева. У кожній вершині верхня половина показує ключ, а нижня -- пріоритет.

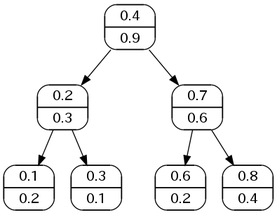
Ви вибираєте \(N\) незалежних випадкових дійсних ключів та пріоритетів у межах від 0 до 1. Знайдіть ймовірність того, що висота декартового дерева, побудованого для цих значень, стане \(h\) (\(h = 0, 1, \ldots, N-1 \)).

Висота дерева визначається як максимальна кількість ребер, яку необхідно пройти, щоб дістатися від якогось листа дерева до його кореня.

Формат вхідних даних

Вам дано єдине ціле число \(N\) (\(1 \le N \le 3 \cdot 10^4\)).

Формат вихідних даних

Виведіть \(N\) рядків. На \(i\)-th рядку виведіть ймовірність того, що висота дерева стане \(i-1\). Абсолютна помилка має бути не більше \(10^{-5}\).

Приклад вхідних даних

1

Приклад вихідних даних

1.0000000000

Приклад вхідних даних

2

Приклад вихідних даних

0.0000000000
1.0000000000

Приклад вхідних даних

3

Приклад вихідних даних

0.0000000000
0.3333333333
0.6666666667