13010. Tree and Constraints
Відправити розв'язок
Бали:
100
Time limit:
2.0s
Memory limit:
250M
Authors:
Problem type
Allowed languages
C++, Java, Pascal, Python
У нас є дерево з \(N\) вершинами, пронумерованими від 1 до \(N\). \(i\)-те ребро в цьому дереві з’єднує вершину \(a_i\) та вершину \(b_i\) .
Розфарбуйте кожен із цих ребер білим або чорним. Існує \(2^{N−1}\) таких способів розфарбовування ребер. Скільки з них задовольняють усі наведені нижче \(M\) обмеження?
- \(i\)-те (\(1≤i≤M\)) обмеження представлено двома цілими числами \(u_i\) та \(v_i\) , які означають, що шлях, що з’єднує вершину \(u_i\) та вершину \(v_i\) , повинен містити принаймні одне ребро, пофарбоване чорним кольором.
Обмеження
- \(2≤N≤50\)
- \(1≤a_i ,b_i ≤N\)
- Граф, поданий у вхідних даних, є деревом.
- \(1≤M≤min(20, N(N−1)/2 )\)
- \(1≤u_i <v_i ≤N\)
- Якщо \(i \neq j\), то \(u_i \neq u_j\) або \(v_i \neq v_j\)
- Усі значення у вхідних даних є цілими числами.
Формат вхідних даних
Перший рядок містить ціле число \(N\).
Наступні \(N-1\) рядки містять цілі числа \(a_i, b_i\)
Далі рядок містить ціле число \(M\).
Наступні \(M\) рядків містять цілі числа \(u_i, v_i\)
Формат вихідних даних
Виведіть кількість способів фарбування ребер, які задовольняють усі \(𝑀\) умов.
Приклад вхідних даних
3
1 2
2 3
1
1 3Приклад вихідних даних
3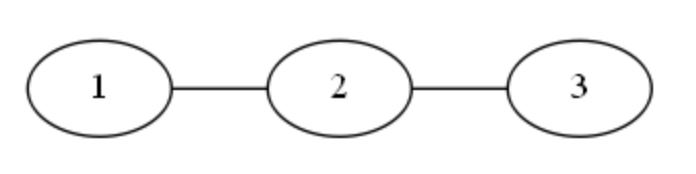
Всі \(𝑀\) обмежень буде виконано, якщо ребра 1 і 2 відповідно пофарбовані (білий, чорний), (чорний, білий) або (чорний, чорний), тому відповідь така 3 .
Приклад вхідних даних
2
1 2
1
1 2Приклад вихідних даних
1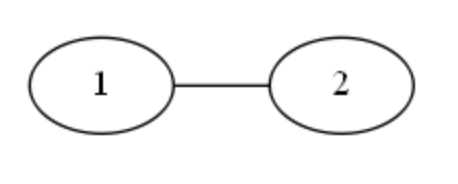
Приклад вхідних даних
5
1 2
3 2
3 4
5 3
3
1 3
2 4
2 5Приклад вихідних даних
9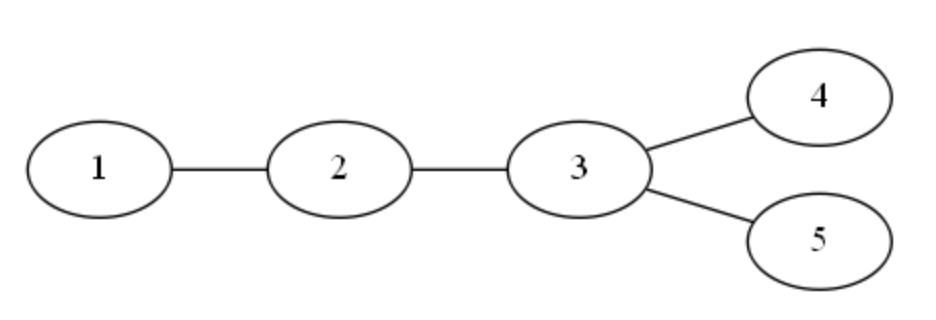
Приклад вхідних даних
8
1 2
2 3
4 3
2 5
6 3
6 7
8 6
5
2 7
3 5
1 6
2 8
7 8Приклад вихідних даних
62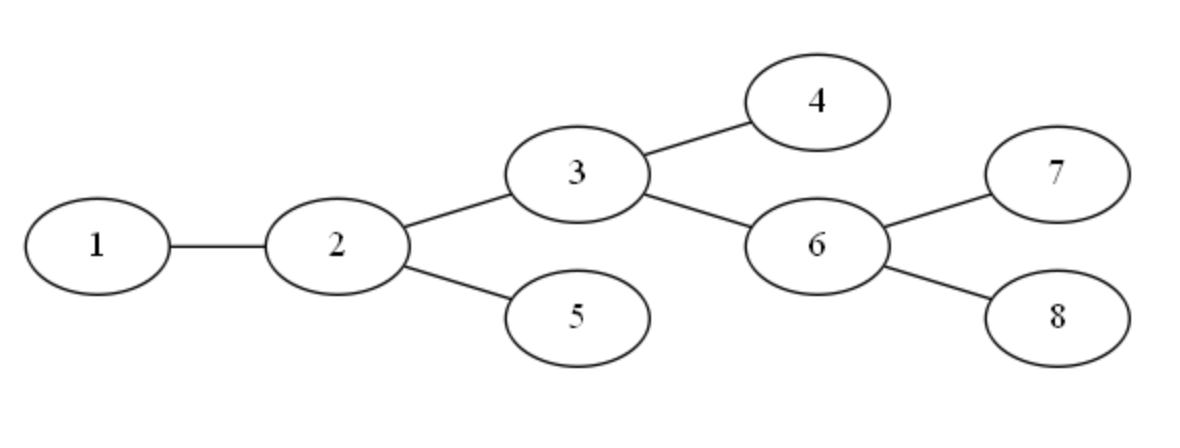
Коментарі