На координатній площині є \(N\) людей, пронумерованих числами від 1 до \(N\).

Особа 1 знаходиться в початку координат.

Вам надається \(M\) частин інформації в такій формі:

• з точки зору особи \(A_i\) ​ особа \(B_i\) ​ знаходиться на відстані \(X_i\) ​ одиниць у додатному напрямку \(x\) і \(Y_i\) ​ одиниць у додатному напрямку \(y\).

Визначте координати кожної людини. Якщо неможливо однозначно визначити координати людини, повідомте про це.

Обмеження

• \(1≤N≤2×10^5\)
• \(0≤M≤2×10^5\)
• \(1≤A_i ​,B_i ≤N\)
• \(A_i ​ \neq B_i\) ​
• \(−10^9 ≤X_i ​ ,Y_i​ ≤10^9\)
• Усі вхідні значення є цілими числами.
• Наведена інформація послідовна.

Формат вхідних даних

Перший рядок містить цілі числа \(N,M\).

Наступні  \(M\) рядків містять цілі числа \(A_i, B_i, X_i, Y_i\).

Формат вихідних даних

Вивести \(N\) рядків.

Якщо координати особи \(i\) не можуть бути однозначно визначені, \(i\)-й рядок має містити undecidable. Якщо їх можна однозначно визначити як \((s_i ​,t_i ​)\), \(i\)-й рядок має містити \(s_i\) ​ та \(t_i\) ​ у такому порядку, розділених пробілом.

Приклад вхідних даних

3 2
1 2 2 1
1 3 -1 -2

Приклад вихідних даних

0 0
2 1
-1 -2

На малюнку нижче показано позиційне співвідношення трьох осіб.

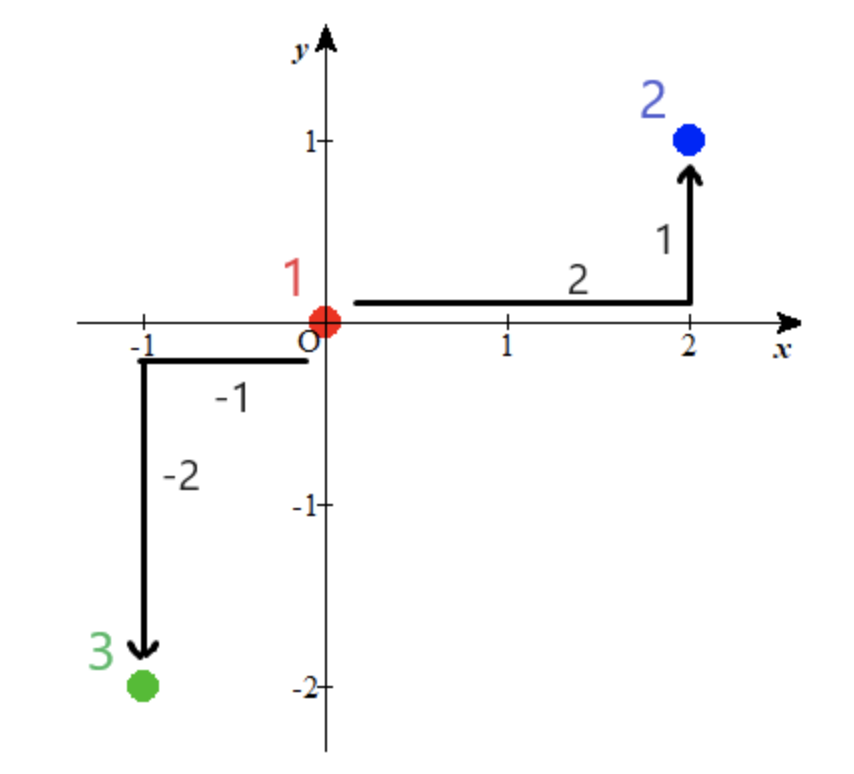
Приклад вхідних даних

3 2
2 1 -2 -1
2 3 -3 -3

Приклад вихідних даних

0 0
2 1
-1 -2

На малюнку нижче показано позиційне співвідношення трьох осіб.

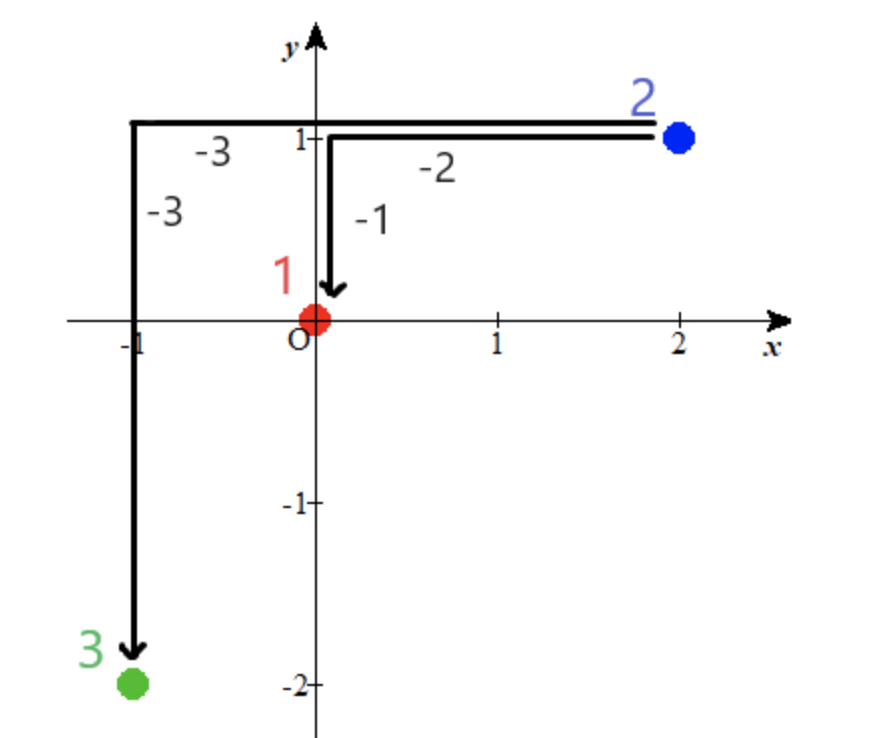
Приклад вхідних даних

5 7
1 2 0 0
1 2 0 0
2 3 0 0
3 1 0 0
2 1 0 0
3 2 0 0
4 5 0 0

Приклад вихідних даних

0 0
0 0
0 0
undecidable
undecidable

Одну й ту саму інформацію можна надати кілька разів, і кілька людей можуть перебувати в тих самих координатах.