У кожному квадраті є сітка 3×3 із числами від 1 до 9 включно. Квадрат у \(i\)-му рядку зверху та \(j\)-му стовпчику зліва \((1≤i≤3,1≤j≤3)\) містить число \(c_{i,j}\).

Одне й те саме число можна писати в різних квадратах, але не в трьох послідовних клітинках по вертикалі, горизонталі або діагоналі. Точніше, гарантується, що \(c_{i,j}\) ​ задовольняє всі наступні умови.

• \(c_{i,1} ​ =c_{i,2} ​ =c_{i,3}\) ​ не виконується для жодного \(1≤i≤3\).
• \(c_{1,j} ​ =c_{2,j} ​ =c_{3,j}\) ​ не виконується для жодного \(1≤j≤3\).
• \(c_{1,1} ​ =c_{2,2} ​ =c_{3,3}\) ​ не виконується.
• \(c_{3,1} ​ =c_{2,2} ​ =c_{1,3}\) ​ не виконується.

Степан побачить числа, записані в кожній клітинці в довільному порядку. Він буде розчарований, коли знайдеться лінія (вертикальна, горизонтальна або діагональна), яка задовольняє наступну умову.

• Перші два квадрати, які він бачить, містять однакове число, але останній квадрат містить інше число.

Знайти ймовірність того, що Степан побачить числа в усіх квадратах, не розчарувавшись.

Обмеження

• \(c_{i,j} ​ ∈{1,2,3,4,5,6,7,8,9}\) \((1≤i≤3,1≤j≤3)\)
• \(c_{i,1} ​ =c_{i,2} ​ =c_{i, 3}\) ​ не виконується для будь-якого \(1≤i≤3\).
• \(c_{1,j} ​ =c_{2,j} ​ =c_{3,j}\) ​ не виконується для жодного \(1≤j≤3\).
• \(c_{1,1} ​ =c_{2,2} ​ =c_{3,3}\) ​ не виконується.
• \(c_{3,1} ​ =c_{2,2} ​ =c_{1,3}\) ​ не виконується.

Формат вхідних даних

Вхідні дані надаються зі стандартного вводу в такому форматі:

Формат вихідних даних

Виведіть один рядок із імовірністю того, що Степан побачить числа в усіх квадратах, не розчарувавшись. Ваша відповідь буде вважатися правильною, якщо абсолютна похибка від справжнього значення не перевищує ~10^{−8}.

Приклад вхідних даних

3 1 9
2 5 6
2 7 1

Приклад вихідних даних

0.666666666666666666666666666667

Наприклад, якщо Степан побачить \(c_{3,1} ​ =2\),\(c_{2,1} ​ =2\),\(c_{1,1} ​ =3\) у цьому порядку, він розчарується.

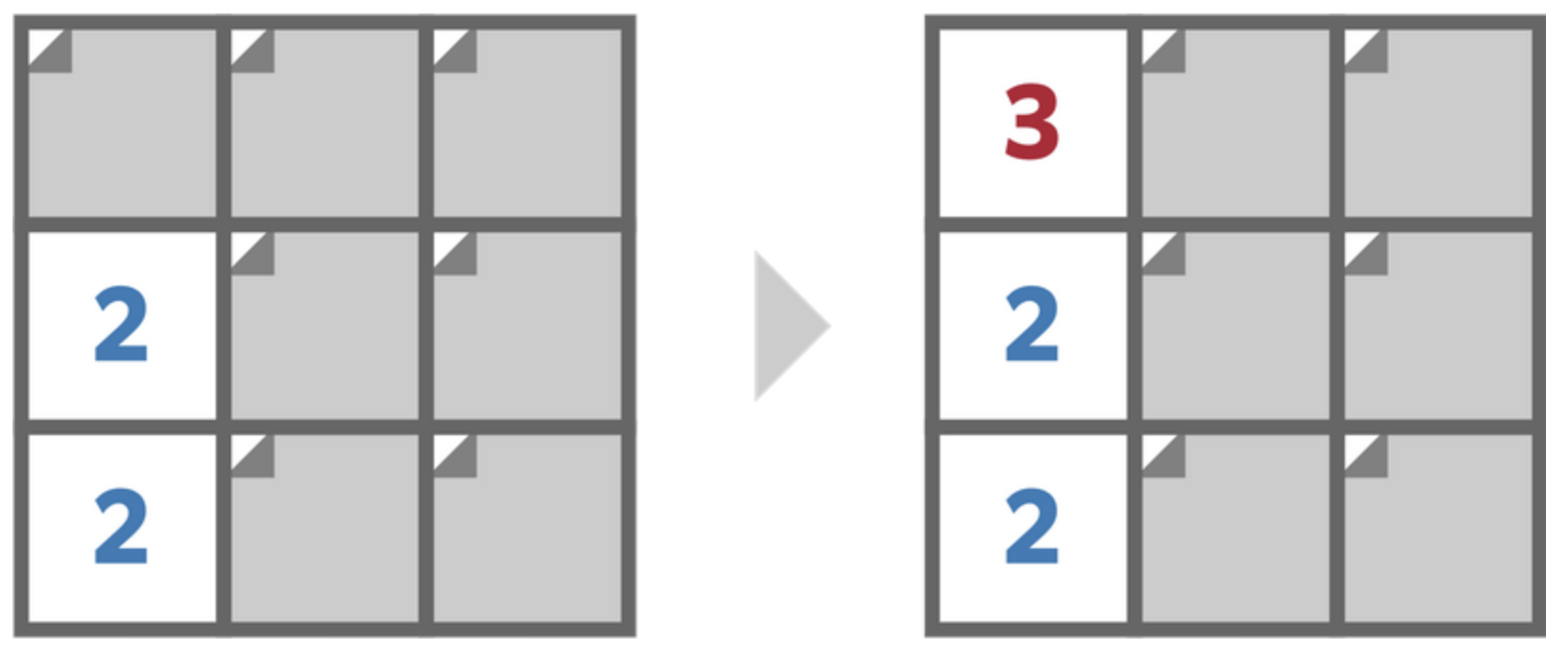
З іншого боку, якщо Степан бачить \(c_{1,1} ​ , c_{1,2} ​ , c_{1,3} ​ , c_{2,1} ​ , c_{2,2} ​ , c_{2,3} ​ , c_{3,1} ​ , c_{3,2} ​,c_{3,3}\) ​ у цьому порядку, він побачить усі числа, не розчаруючись.

Імовірність того, що Степан побачить усі числа, не розчарувавшись, дорівнює 3/2 .

Ваша відповідь буде вважатися правильною, якщо абсолютна похибка від справжнього значення становить не більше \(10^{−8}\), тому такі виводи, як 0,666666657 і 0,666666676, також будуть прийняті.

Приклад вхідних даних

7 7 6
8 6 8
7 7 6

Приклад вихідних даних

0.004982363315696649029982363316

Приклад вхідних даних

3 6 7
1 9 7
5 7 5

Приклад вихідних даних

0.4