На координатній площині розкладено \(N\) прямокутних аркушів.

Кожна сторона прямокутної області, покритої кожним аркушем, паралельна осі \(x\) або \(y\). Зокрема, \(i\)-й аркуш охоплює саме область, яка задовольняє \(A_i ≤x≤B_i\) ​ та \(C_i ≤y≤D_i ​\).

Нехай \(S\) — площа області, покритої одним або кількома листами. Можна довести, що \(S\) є цілим числом при заданих обмеженнях.

Виведіть \(S\) як ціле число.

Обмеження

• \(2≤N≤100\)
• \(0≤A_i ​ <B_i ≤100\)
• \(0≤C_i ​ <D_i ≤100\)
• Усі вхідні значення є цілими числами.

Формат вхідних даних

Перший рядок містить ціле число \(N\).

Наступні  \(N\) рядків містять цілі числа \(A_i,B_i,C_i,D_i\).

Формат вихідних даних

У вихідний потік виведіть відповідь.

Приклад вхідних даних

3
0 5 1 3
1 4 0 5
2 5 2 4

Приклад вихідних даних

20

Три аркуші охоплюють наступні регіони.

Тут червоний, жовтий і синій позначають області, охоплені першим, другим і третім аркушами відповідно.

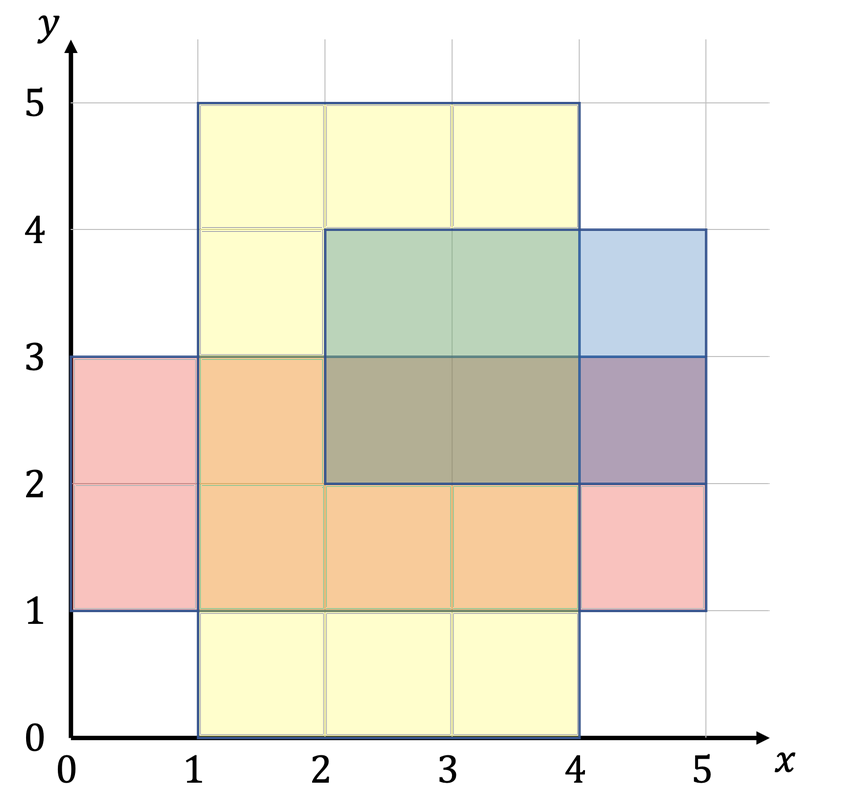
Отже, площа області, покритої одним або кількома аркушами, дорівнює S=20.

Приклад вхідних даних

2
0 100 0 100
0 100 0 100

Приклад вихідних даних

10000

Приклад вхідних даних

3
0 1 0 1
0 3 0 5
5 10 0 10

Приклад вихідних даних

65