12130. Знайди це
Існує орієнтований граф з \(N\) вершинами і \(N\) ребрами. \(i\)-те ребро йде від вершини \(i\) до вершини \(A_i\) . (Обмеження гарантують, що \(i \neq A_i \).)
Знайдіть орієнтований цикл без однієї і тієї ж вершини, що з’являється кілька разів.
Можна показати, що розв’язок існує при обмеженнях цієї задачі.
Примітки. Послідовність вершин \(B=(B_1 ,B_2 ,…,B_M )\) називається спрямованим циклом, якщо виконуються всі наступні умови:
- \(M≥2\)
- Ребро від вершини \(B_i\) до вершини \(B_{i+1}\) існує. \((1≤i≤M−1)\)
- Ребро від вершини \(B_M\) до вершини \(B_1\) існує.
- Якщо \(i \neq j\), то \(B_i \neq B_j \).
Обмеження
- Усі вхідні значення є цілими числами.
- \(2≤N≤2×10^5\)
- \(1≤A_i ≤N\)
- \(A_i \neq i\)
Формат вхідних даних
Перший рядок містить ціле число \(N\).
Наступний рядок містить цілі числа \(A_i\).
Формат вихідних даних
Виведіть розв’язок у такому форматі:
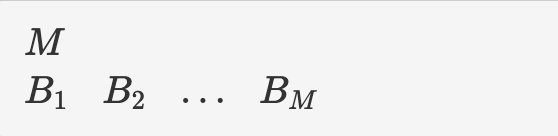
\(M\) — кількість вершин, а \(B_i\) — \(i\)-та вершина в спрямованому циклі.
Якщо існує кілька рішень, будь-яке з них буде прийнято.
Приклад вхідних даних
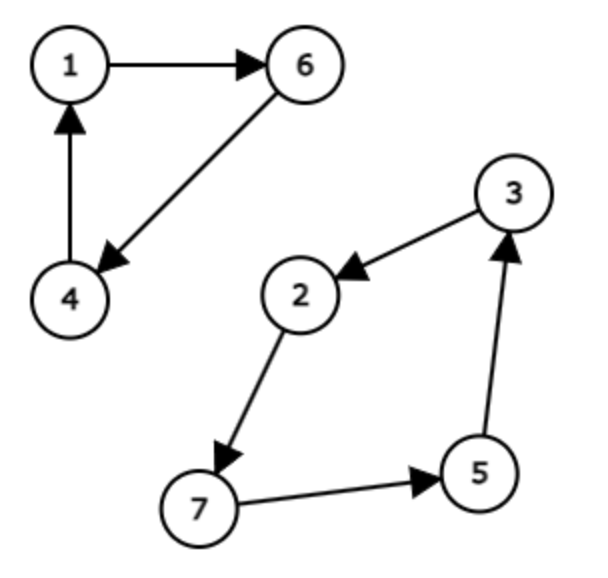
7
6 7 2 1 3 4 5Приклад вихідних даних
4
7 5 3 27→5→3→2→7 справді є спрямованим циклом.
Ось інші прийнятні результати:
4
2 7 5 3
3
4 1 6Приклад вхідних даних
2
2 1Приклад вихідних даних
2
1 2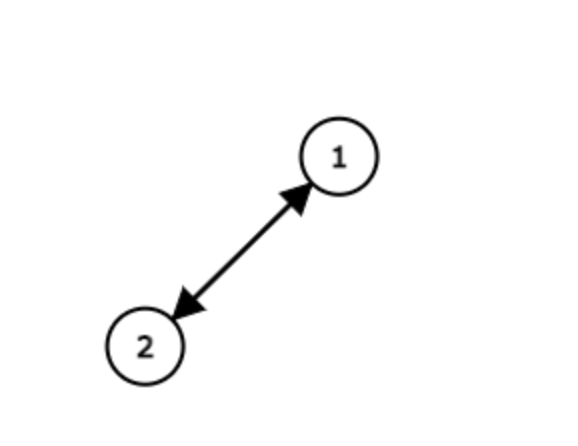
Приклад вхідних даних
8
3 7 4 7 3 3 8 2Приклад вихідних даних
3
2 7 8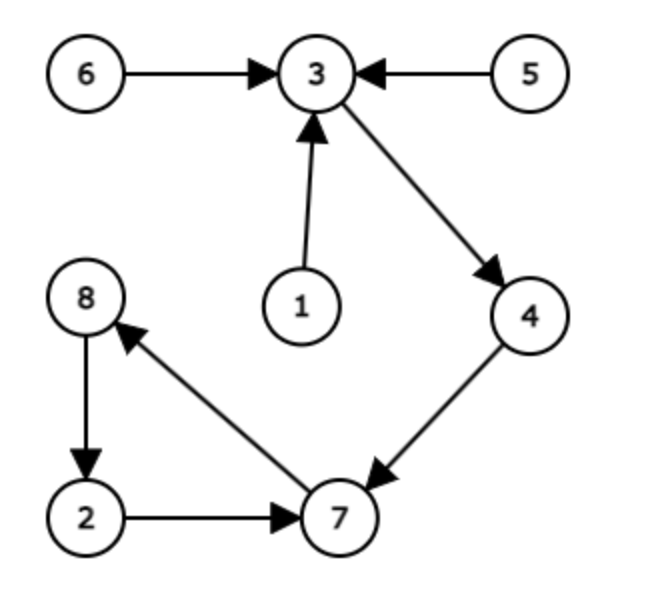
Коментарі