12127. Розбити на команди

Відправити розв'язок
Бали: 100
Time limit: 2.0s
Memory limit: 500M
Authors:
admin, admin2
Problem type
Allowed languages
C++, Java, Pascal, Python

Є \(N\) спортсменів. Серед них \(M\) несумісних пар. \(i\)-та несумісна пара \((1≤i≤M)\) – це \(A_i\)-й і \(B_i\)-й гравці.

Ви розділите гравців на \(T\) команд. Кожен гравець має належати точно до однієї команди, і кожна команда має мати одного або кількох гравців. Крім того, для кожного \(i=1,2,…,M\) гравці \(A_i\) ​ та \(B_i\) не повинні належати до однієї команди.

Знайдіть кількість способів виконання цих умов. Тут два дивізіони вважаються різними, коли в одному дивізіоні є два гравці, які належать до однієї команди, а в іншій – до різних команд.

Обмеження

  • \(1\leq T\leq N\leq10\)
  • \(0\leq M\leq\dfrac{N(N-1)}2\)
  • \(1\leq A_i\lt B_i\leq N\ (1\leq i\leq M)\)
  • \((A_i,B_i)\neq (A_j,B_j)\ (1\leq i\lt j\leq M)\)
  • Усі вхідні значення є цілими числами.

    • Формат вхідних даних

    Перший рядок містить цілі числа \(N,T,M\).

    Наступні  \(M\) рядків містять цілі числа \(A_i, B_i\).

    Формат вихідних даних

    У вихідний потік виведіть відповідь.

    Приклад вхідних даних

    5 2 2
1 3
3 4

    Приклад вихідних даних

    4

    Наступні чотири дивізіони задовольняють умови.

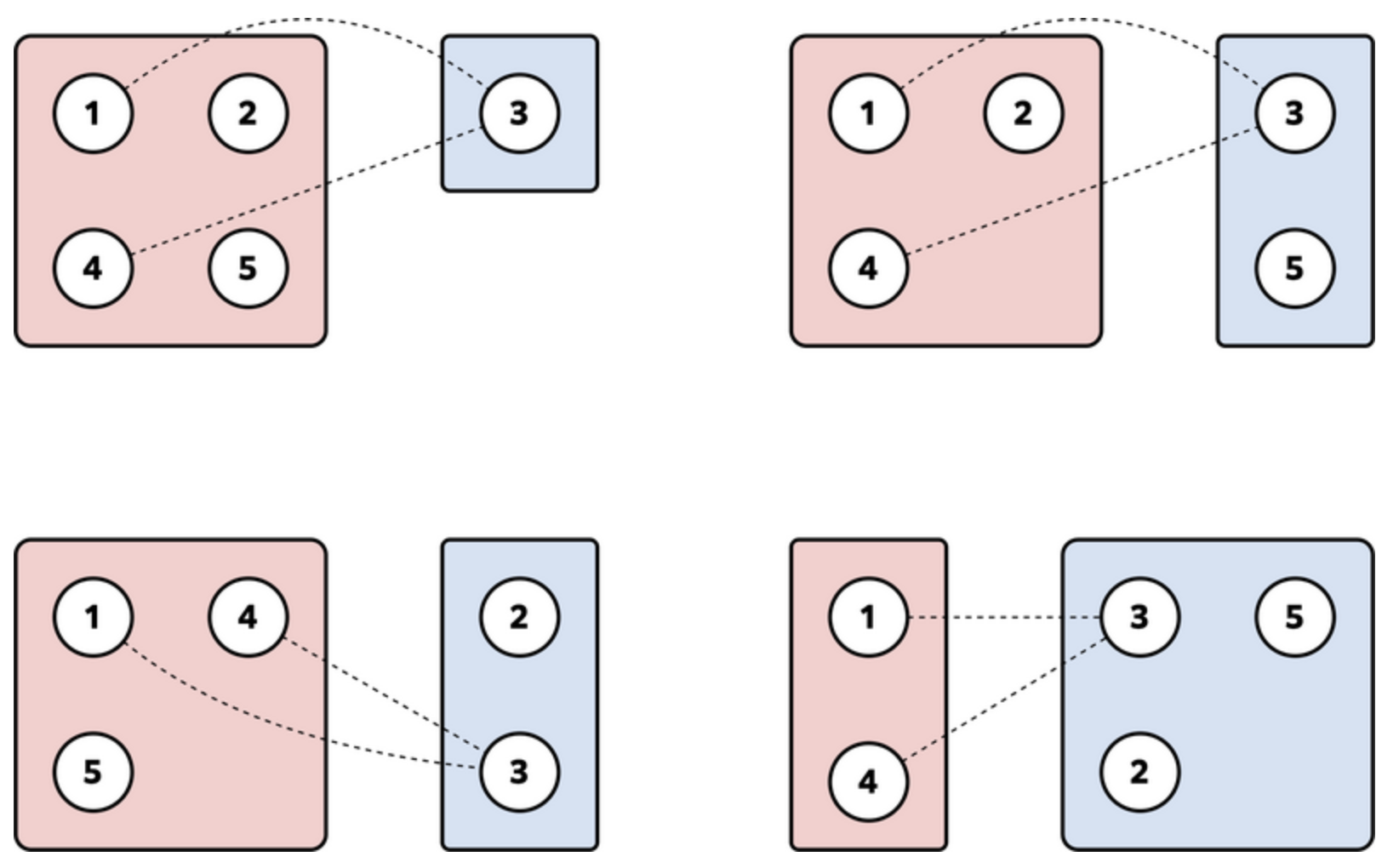
    Приклад вхідних даних

    5 1 2
1 3
3 4

    Приклад вихідних даних

    0

    Приклад вхідних даних

    6 4 0

    Приклад вихідних даних

    65

    Приклад вхідних даних

    10 6 8
5 9
1 4
3 8
1 6
4 10
5 7
5 6
3 7

    Приклад вихідних даних

    8001

    Коментарі

    Ще немає коментарів.