IT-Shop має \(N\) товарів. Ціна \(i\)-го продукту \((1≤i≤N)\) дорівнює \(P_i ​\). \(i\)-й продукт \((1≤i≤N)\) має \(C_i\) ​ функцій. \(j\)-та функція \((1≤j≤C_i ​)\) \(i\)-го продукту \((1≤i≤N)\) представлена як ціле число \(F_{i,j}\) ​ від 1 до \(M\) включно.

Степан цікавиться, чи існує продукт, який абсолютно кращий за інший. Якщо \(i\) та \(j\) \((1≤i,j≤N)\) такі, що \(i\)-й та \(j\)-й продукти задовольняють усі наступні умови, виведіть Yes; інакше виведіть No

• \(P_i ≥P_j \).
• \(j\)-й продукт виконує всі функції \(i\)-го продукту.
• \(P_i ​ >P_j\) ​ або \(j\)-й продукт має одну чи декілька функцій, яких не має \(i\)-й продукт.

Обмеження

• \(2≤N≤100\)
• \(1≤M≤100\)
• \(1≤P_i ​ ≤10^5\)  \((1≤i≤N)\)
• \(1≤C_i ≤M\) \((1≤i≤N)\)
• \(1≤F_{i,1} ​<F_{I ,2} ​ <⋯<F_{i,C_i} ​ ≤M\) \((1≤i≤N)\)
• Усі вхідні значення є цілими числами.

Формат вхідних даних

Вхідні дані надаються зі стандартного потоку в такому форматі:

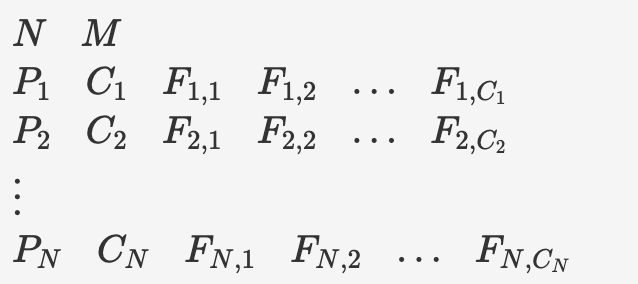
Формат вихідних даних

У вихідний потік виведіть відповідь.

Приклад вхідних даних

5 6
10000 2 1 3
15000 3 1 2 4
30000 3 1 3 5
35000 2 1 5
100000 6 1 2 3 4 5 6

Приклад вихідних даних

Yes

\((i,j)\)=(4,3) задовольняє всі умови. Жодна інша пара їх не задовольняє.

Наприклад, для \((i,j)\)=(4,5) \(j\)-й продукт виконує всі функції \(i\)-го, але \(P_i ​ <P_j ​\) , тому він не є строго вищим.

Приклад вхідних даних

4 4
3 1 1
3 1 2
3 1 2
4 2 2 3

Приклад вихідних даних

No

Приклад вхідних даних

20 10
72036 3 3 4 9
7716 4 1 2 3 6
54093 5 1 6 7 8 10
25517 7 3 4 5 6 7 9 10
96930 8 2 3 4 6 7 8 9 10
47774 6 2 4 5 6 7 9
36959 5 1 3 4 5 8
46622 7 1 2 3 5 6 8 10
34315 9 1 3 4 5 6 7 8 9 10
54129 7 1 3 4 6 7 8 9
4274 5 2 4 7 9 10
16578 5 2 3 6 7 9
61809 4 1 2 4 5
1659 5 3 5 6 9 10
59183 5 1 2 3 4 9
22186 4 3 5 6 8
98282 4 1 4 7 10
72865 8 1 2 3 4 6 8 9 10
33796 6 1 3 5 7 9 10
74670 4 1 2 6 8

Приклад вихідних даних

Yes