Ми маємо неорієнтований граф з \((N_1 ​+N_2 ​ )\) вершинами та \(M\) ребрами. Для \(i=1,2,…,M\) \(i\)-те ребро з’єднує вершину \(a_i\) ​ та \(b_i ​\). Наступні властивості гарантуються:

• \(Вершина \)u\( і вершина \)v\( зв’язані для всіх цілих чисел \)u\( і \)v\( з \)1≤u,v≤N_1~ ​.
• Вершина \(u\) і вершина \(v\) зв’язані, для всіх цілих чисел \(u\) і \(v\) з \(N_1 ​+ 1≤u,v≤N_1 ​+ N_2 ​\) .
• Вершина 1 і вершина \((N_1 ​+ N_2 )\) роз'єднані.

Виконайте наступну операцію рівно один раз:

• виберіть ціле число \(u\) з \(1≤u≤N_1\) ​ і ціле число \(v\) з \(N_1 ​+ 1≤v≤N_1 ​+ N_2\) ​ і додайте ребро, що сполучає вершину \(u\) і вершину \(v\). Ми можемо показати, що вершина 1 і вершина \((N_1 ​+ N_2 ​ )\) завжди зв'язані в отриманому графі; отже, нехай \(d\) буде мінімальною довжиною (кількістю ребер) шляху між вершиною 1 і вершиною \((N_1 ​+ N_2 ​ )\).

Знайдіть максимально можливе \(d\), отримане в результаті додавання відповідного ребра, яке потрібно додати.

Дві вершини \(u\) і \(v\) неорієнтованого графа називаються з’єднаними тоді і тільки тоді, коли існує шлях між вершиною \(u\) і вершиною \(v\).

Обмеження

• \(1≤N_1 ​,N_2 ​ ≤1,5×10^5\)
• \(0 ≤M≤3×10^5\)
• \(1≤a_i ≤b_i ≤N_1 ​+ N+2\) ​
• \((a_i ,b_i ) \neq (a_j ,b_j ​)\), якщо \(i \neq j\).
• Вершина \(u\) і вершина \(v\) є зв’язними для всіх цілих чисел \(u\) і \(v\) таких, що \(1≤u,v≤N_1 ​\).
• Вершина \(u\) і вершина \(v\) є зв’язними для всіх цілих чисел \(u\) і \(v\) таких, що \(N_1 ​+ 1≤u,v≤N+1 ​+ N_2 ​ \).
• Вершина 1 і вершина \((N_1 ​+ N_2 )\) роз'єднані.
• Усі вхідні значення є цілими числами.

Формат вхідних даних

Перший рядок містить цілі числа \(N_1, N_2,M\).

Наступні  \(M\) рядків містять цілі числа \(a_i, b_i\).

Формат вихідних даних

У вихідний потік виведіть відповідь.

Приклад вхідних даних

3 4 6
1 2
2 3
4 5
4 6
1 3
6 7

Приклад вихідних даних

5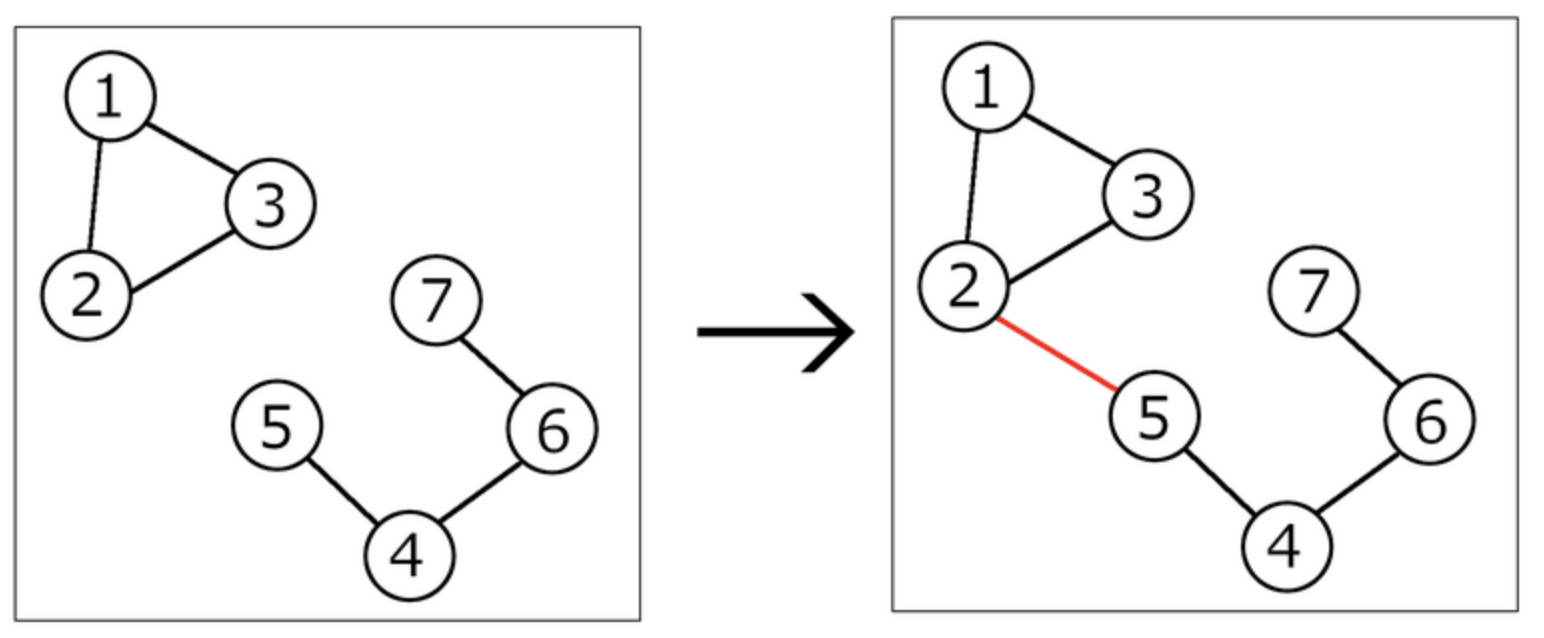

Приклад вхідних даних

7 5 20
10 11
4 5
10 12
1 2
1 5
5 6
2 4
3 5
9 10
2 5
1 4
11 12
9 12
8 9
5 7
3 7
3 6
3 4
8 12
9 11

Приклад вихідних даних

4