12080. Хрестики
У нас є сітка з \(H\) горизонтальних рядків і \(W\) вертикальних стовпців. Ми позначимо \((i,j)\) комірку в \(i\)-му рядку зверху та \(j\)-му стовпчику зліва від сітки.
Кожна клітинка сітки містить символ # або . . Нехай \(C[i][j]\) — символ, написаний на \((i,j)\). Для цілих чисел \(i\) та \(j\) таких, що принаймні одне з \(1≤i≤H\) та \(1≤j≤W\) порушується, ми визначаємо \(C[i][j]\) як ..
\((4n+1)\) квадрати, що складаються з \((a,b )\) і \((a+d,b+d)\),\((a+d,b−d)\),\((a−d,b+d)\),\((a−d,b−d)\) \((1≤d≤n,1≤n)\), називаються хрестиком розміру \(n\) з центром \((a,b)\) тоді і тільки тоді, коли задовольняються всі наступні умови:
- \(C[a][b]\) дорівнює #.
- \(C[a+d][b+d]\),\(C[a+d][b−d]\),\(C[a−d][b+d]\) і \(C[a−d][b−d]\) є #, для всіх цілих \(d\) таких, що \(1≤d≤n\),
- принаймні один із \(C[a+n+1][b+n+1]\),\(C[a+n+1][b−n−1]\),\(C[a−n−1][b+n+1]\) та \(C[a −n−1][b−n−1]\) дорівнює ..
Наприклад, сітка на наступному малюнку має хрестик розміру 1 з центром (2,2) та інший хрестик розміру 2 з центром (3,7).
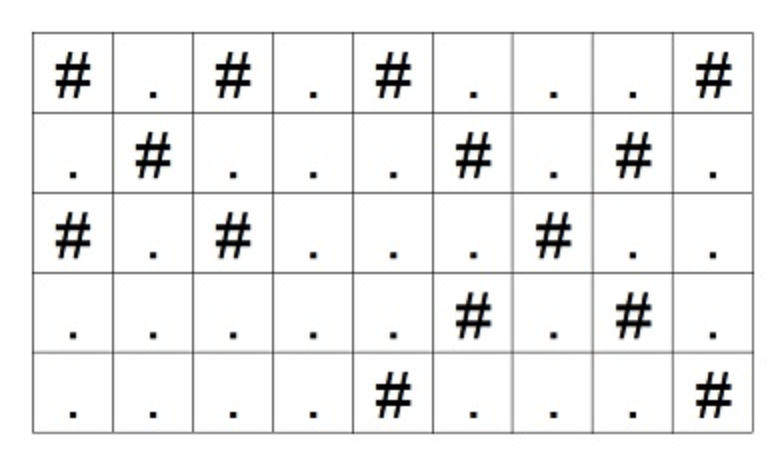
На сітці кілька хрестиків. У клітинках не пишеться #, за винятком тих, які містять хрестик. Крім того, жодні два квадрати, які складаються з двох різних хрестів, не мають спільного кута.
Дві сітки на наступному малюнку є прикладами сіток, де два квадрати, що містять різні хрести, мають спільний кут; такі сітки не надаються як вхідні дані. Наприклад, ліва сітка недійсна, оскільки (3,3) і (4,4) мають спільний кут.
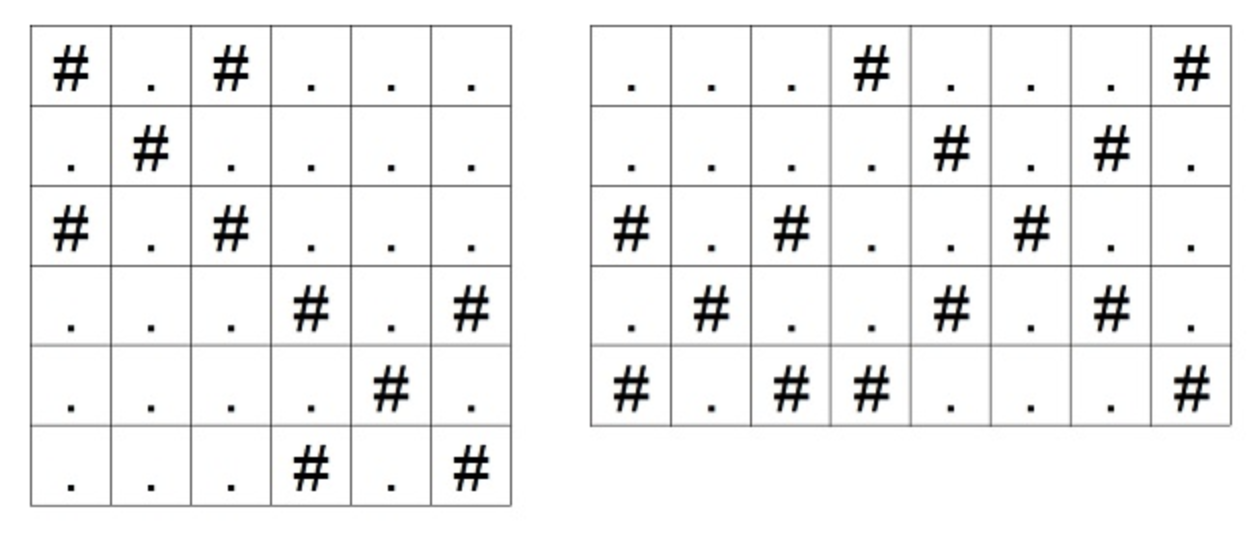
Нехай \(N=min(H,W)\), а \(S_n\) — кількість хрестиків розміру \(n\). Знайдіть \(S_1 , S_2 ,…, S_N \) .
Обмеження
- \(3≤H,W≤100\)
- \(C[i][j]\) дорівнює # або . .
- Немає двох різних квадратів, які складаються з двох різних хрестів, спільного кута.
- \(H\) і \(W\) — цілі числа.
Формат вхідних даних
Перший рядок містить цілі числа \(H,W\).
Наступні \(N\) рядків містять \(C[i][j]\).
Формат вихідних даних
У вихідний потік виведіть \(S_1 , S_2 ,… S_N \) , розділивши їх пробілами.
Приклад вхідних даних
5 9
#.#.#...#
.#...#.#.
#.#...#..
.....#.#.
....#...#Приклад вихідних даних
1 1 0 0 0Як описано в умові задачі, є хрестик розміру 1 з центром (2,2) і інший розміром 2з центром (3,7).
Приклад вхідних даних
3 3
...
...
...Приклад вихідних даних
0 0 0Приклад вхідних даних
3 16
#.#.....#.#..#.#
.#.......#....#.
#.#.....#.#..#.#Приклад вихідних даних
3 0 0Приклад вхідних даних
15 20
#.#..#.............#
.#....#....#.#....#.
#.#....#....#....#..
........#..#.#..#...
#.....#..#.....#....
.#...#....#...#..#.#
..#.#......#.#....#.
...#........#....#.#
..#.#......#.#......
.#...#....#...#.....
#.....#..#.....#....
........#.......#...
#.#....#....#.#..#..
.#....#......#....#.
#.#..#......#.#....#Приклад вихідних даних
5 0 1 0 0 0 1 0 0 0 0 0 0 0 0
Коментарі