Вивчаючи Канбун, Степану важко визначити порядок читання слів. Допоможіть йому!

Існує \(N\) цілих чисел від 1 до \(N\), розташованих у рядку в порядку зростання. Між ними позначки M "レ". \(i\)-та позначка «レ» знаходиться між цілим числом \(a_i\) ​ і цілим числом \((a_i ​+1)\).

Ви зчитуєте кожне з \(N\) цілих чисел один раз за допомогою наступної процедури.

• Розглянемо неорієнтований граф \(G\) з \(N\) вершинами, пронумерованими від 1 до \(N\) і \(M\) ребрами. \(i\)-те ребро сполучає вершину \(a_i\) ​ і вершину \((a_i ​+ 1)\).
• Повторюйте наступну операцію, доки не залишиться непрочитане ціле число:
• нехай \(x\) буде мінімальним непрочитаним цілим числом. Виберемо компонент зв'язності \(C\), що містить вершину \(x\), і прочитаємо всі номери вершин, що містяться в \(C\), у порядку спадання.

Наприклад, припустимо, що цілі числа та позначки "レ" розташовані в такому порядку:

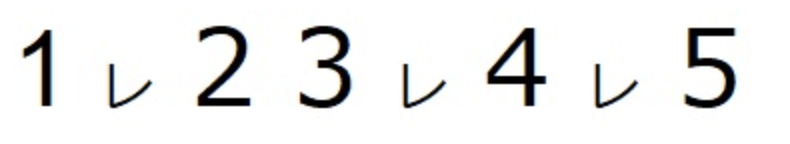
(У цьому випадку \(N\)=5,\(M\)=3 і \(a=(1,3,4)\).)

Тоді порядок читання цілих чисел визначається як 2, 1, 5, 4 і 3 таким чином:

• спочатку мінімальне непрочитане ціле число дорівнює 1, а зв’язний компонент \(G\), що містить вершину 1, має вершини {1, 2}, тому 2 і 1 читаються в такому порядку.
• Тоді мінімальне непрочитане ціле число дорівнює 3, а зв’язний компонент \(G\), що містить вершину 3, має вершини {3,4,5}, тому 5, 4 і 3 зчитуються в такому порядку.
• Тепер, коли всі цілі числа прочитано, завершіть процедуру.

Дано \(N,M\) і \((a_1 ​,a_2 ​ ,…,a_M ​)\). Виведіть порядок читання \(N\) цілих чисел.

Що таке зв’язний компонент? Підграфом графа називається граф, отриманий шляхом вибору деяких вершин і ребер з вихідного графа. Граф називається звʼязним тоді і тільки тоді, коли можна пересуватися між будь-якими двома вершинами графа через ребра. Зв’язний компонент — зв’язний підграф, який не міститься в жодному більшому зв’язному підграфі.

Обмеження

• \(1≤N≤100\)
• \(0≤M≤N−1\)
• \(1≤a_1 ​ <a_2 ​ <⋯<a_M ​ ≤N−1\)
• Усі значення у вхідних даних є цілими числами.

Формат вхідних даних

Перший рядок містить цілі числа \(N,M\).

Наступний   рядок містить \(M\) цілих чисел \(a_i\).

Формат вихідних даних

У вихідний потік виведіть відповідь у такому форматі, де \(p_i\) ​ — це \(i\)-те ціле число для читання.

p_1 p_2 ... p_N

Приклад вхідних даних

5 3
1 3 4

Приклад вихідних даних

2 1 5 4 3

Цей приклад описаний в умові задачі.

Приклад вхідних даних

5 0

Приклад вихідних даних

1 2 3 4 5

Знак "レ" може бути відсутнім.

Приклад вхідних даних

10 6
1 2 3 7 8 9

Приклад вихідних даних

4 3 2 1 5 6 10 9 8 7