Вам дано простий неорієнтований граф з \(N\) вершинами та \(M\) ребрами. Вершини пронумеровані \(1,2,…,N\), а ребра – \(1,2,…,M\).

Ребро \(i\) \((i=1,2,…,M)\) з’єднує вершини \(u_i\) ​ та \(v_i ​ \).

Визначте, чи є цей граф контурним.

Що таке простий неорієнтований граф? Простий неорієнтований граф — це граф без петель або множинних ребер, ребра яких не мають напрямку.

Що таке граф контурний? Граф з \(N\) вершинами, пронумерованими \(1,2,…,N\), називається графом контурним тоді і тільки тоді, коли існує послідовність \((v_1 ,v_2 ,…,v_N )\), яка є перестановкою \((1 ,2,…,N)\) і задовольняє такі умови:

• Для всіх \(i=1,2,…,N−1\) існує ребро, що з’єднує вершини \(v_i\) ​ та \(v_{i+1}\) ​.
• Якщо цілі числа \(i\) та \(j\) задовольняють \(1≤i,j≤N\) та \(∣i−j∣≥2\), то не існує ребра, яке з’єднує вершини \(v_i\) ​ та \(v_j ​\).

Обмеження

• \(2≤N≤2×10^5\)
• \(0≤M≤2×10^5\)
• \(1≤u_i ​,v_i ​ ≤N\)\((i=1,2,…,M)\)
• Усі значення у вхідних даних є цілими числами.
• Граф, поданий у вхідних даних, простий.

Формат вхідних даних

Перший рядок містить цілі числа \(N,M\).

Наступні  \(M\) рядків містять цілі числа \(u_i, v_i\).

Формат вихідних даних

У вихідний потік виведіть відповідь: Yes або No.

Приклад вхідних даних

4 3
1 3
4 2
3 2

Приклад вихідних даних

Yes

Нижче наведено наведений граф, який є графом контурним.

Приклад вхідних даних

2 0

Приклад вихідних даних

No

Приклад вхідних даних

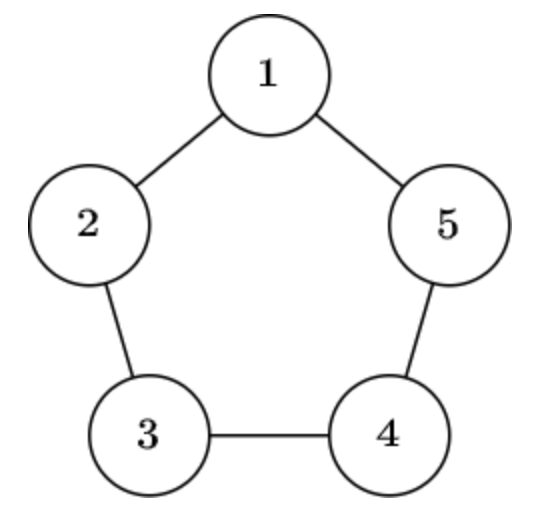
5 5
1 2
2 3
3 4
4 5
5 1

Приклад вихідних даних

No

Нижче наведено наведений граф, який не є графом контурним.