Вам дано простий неорієнтований граф з \(N\) вершинами, пронумерованими від 1 до \(N\), і \(M\) ребрами, пронумерованими від 1 до \(M\). Ребро \(i\) з’єднує вершину \(u_i\) ​ та вершину \(v_i\) ​.

Знайдіть кількість компонент зв’язності в цьому графі.

Простий неорієнтований граф — це простий граф із неорієнтованими ребрами. Граф є простим тоді і тільки тоді, коли він не має петлі чи мультиребра. Підграф графа — це граф, утворений з деяких вершин і ребер цього графа. Граф є зв’язним тоді і тільки тоді, коли можна пересуватися між кожною парою вершин через ребра. Зв'язний компонент - це зв'язний підграф, який не є частиною жодного більшого зв'язного підграфа.

Обмеження

• \(1≤N≤100\)
• \(0≤M≤ N(N−1)/2\) ​
• \(1≤u_i ​ ,v_i ​ ≤N\)
• Даний граф простий.
• Усі значення у вхідних даних є цілими числами.

Формат вхідних даних

Перший рядок містить цілі числа \(N,M\).

Наступні  \(M\) рядків містять цілі числа \(u_i, v_i\).

Формат вихідних даних

У вихідний потік виведіть відповідь.

Приклад вхідних даних

5 3
1 2
1 3
4 5

Приклад вихідних даних

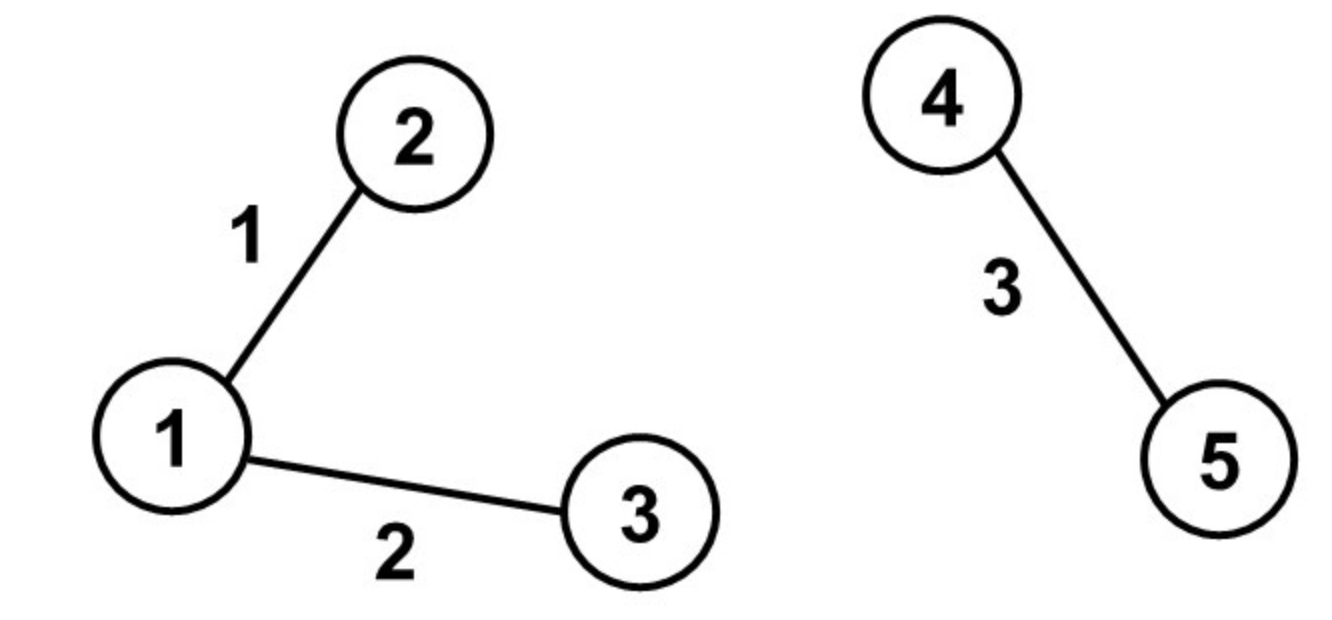
2

Даний граф містить такі дві зв’язані компоненти:

• підграф, утворений з вершин 1, 2, 3, а ребра 1, 2;
• підграф, утворений з вершин 4, 5, і ребро 3.

Приклад вхідних даних

5 0

Приклад вихідних даних

5

Приклад вхідних даних

4 6
1 2
1 3
1 4
2 3
2 4
3 4

Приклад вихідних даних

1