Існує дерево \(T\) з \(N\) вершинами. \(i\)-е ребро (\(1\leq i\leq N-1\)) сполучає вершину \(U_i\) і вершину \(V_i\).

Вам задано дві різні вершини \(X\) і \(Y\) у \(T\). Перерахуйте всі вершини вздовж простого шляху від вершини \(X\) до вершини \(Y\) по порядку, включаючи кінцеві точки.

Можна довести, що для будь-яких двох різних вершин \(a\) і \(b\) в дереві існує єдиний простий шлях від \(a\) до \(b\).

Що таке простий шлях? Для вершин \(X\) і \(Y\) в графі \(G\) шлях від вершини \(X\) до вершини \(Y\) є послідовністю вершин \(v_1,v_2, \ldots, v_k\) так, що \(v_1=X\), \(v_k=Y\) і \(v_i\) \(v_{i+1}\) з’єднані ребром для кожного \(1\leq i\leq k-1\). Крім того, якщо всі \(v_1,v_2, \ldots, v_k\) різні, шлях називається простим шляхом від вершини \(X\) до вершини \(Y\).

Обмеження

• \(1\leq N\leq 2\times 10^5\)
• \(1\leq X,Y\leq N\)
• \(X\neq Y\)
• \(1\leq U_i,V_i\leq N\)
• Усі значення у вхідних даних є цілими числами.
• Даний граф є деревом.

Формат вхідних даних

Перший рядок містить цілі числа \(N,X,Y\)

Наступні  \(N-1\) рядків містять цілі числа \(U_i, V_i\)

Числа у рядках розділяються пропуском.

Формат вихідних даних

У вихідний потік виведіть індекси всіх вершин уздовж простого шляху від вершини \(X\) до вершини \(Y\) по порядку, з пробілами між ними.

Примітка

До прикладу 1:

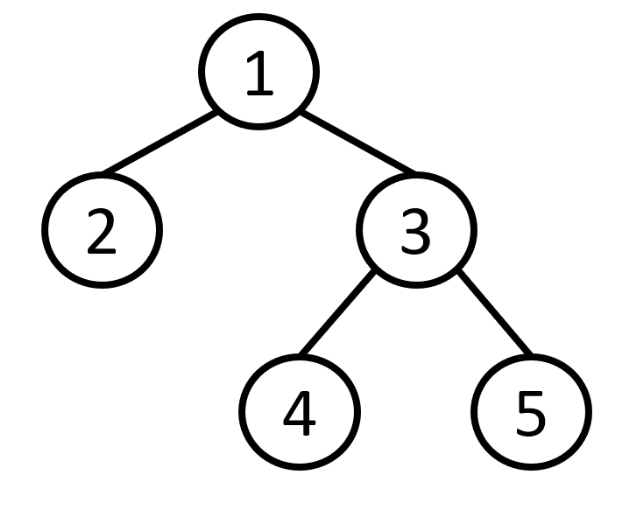
Приклад вхідних даних

5 2 5
1 2
1 3
3 4
3 5

Приклад вихідних даних

2 1 3 5

Приклад вхідних даних

6 1 2
3 1
2 5
1 2
4 1
2 6

Приклад вихідних даних

1 2