11877. Кеглі
Кеглі для боулінгу пронумеровані від 1 до 10. На наступному малюнку показано розташування кеглів зверху:
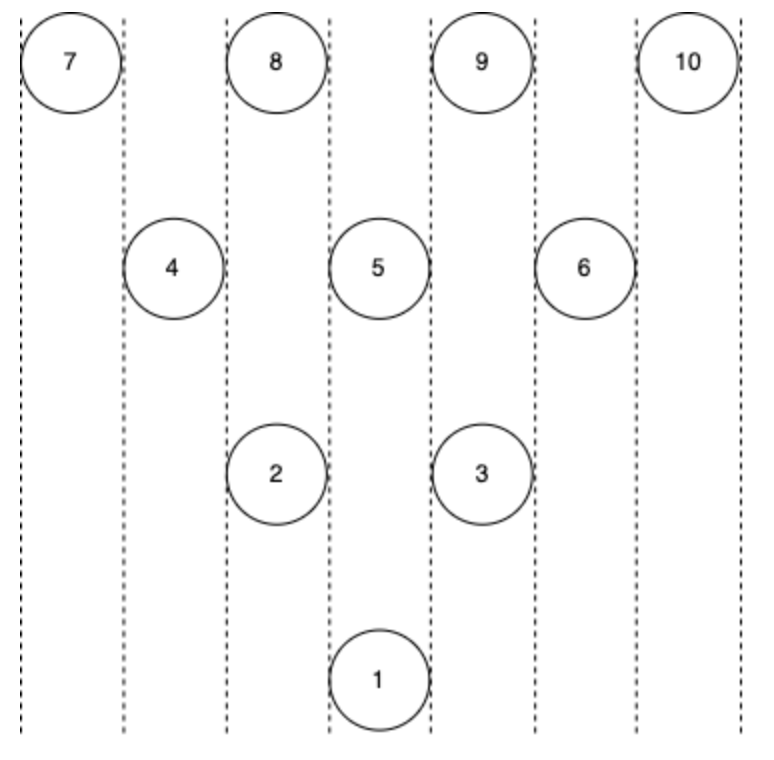
Кожну частину між двома пунктирними лініями на малюнку назвемо стовпчиком.
Наприклад, кеглі 1 і 5 належать до одного стовпця, а також 3 і 9. Коли деякі з кеглів збиті, може виникнути особлива ситуація, яка називається розколом. Розташування кеглів вважається розколом, якщо задовольняються обидві наступні умови:
1 збитий.
Існує два різних стовпці, які задовольняють обидві наступні умови:
Кожна колона має один або кілька стоячих кеглів.
- Між цими колонами існує стовпчик, у якому всі кеглі в стовпчику збиті.
Дивіться також зразки входів і виходів для прикладів.
Тепер вам надано розташування кеглів у вигляді рядка \(S\) довжиною 10. Для \(i = 1, \dots, 10\), \(i\)-й символ \(S\) дорівнює 0, якщо кегель \(i\) збитий, і дорівнює 1, якщо він стоїть.
Визначте, чи розміщення кеглів, представлене \(S\), є розколом.
Обмеження
- \(S\) — це рядок довжиною 10, що складається з 0 і 1.
Формат вхідних даних
Вхідний потік містить рядок \(S\)
Формат вихідних даних
У вихідний потік вивести \(Yes\) або \(No\) - відповідь на поставлене завдання
Примітка
До прикладу 1:
На малюнку нижче збиті кеглі пофарбовані в сірий колір, а стоячі кеглі пофарбовані в білий колір:
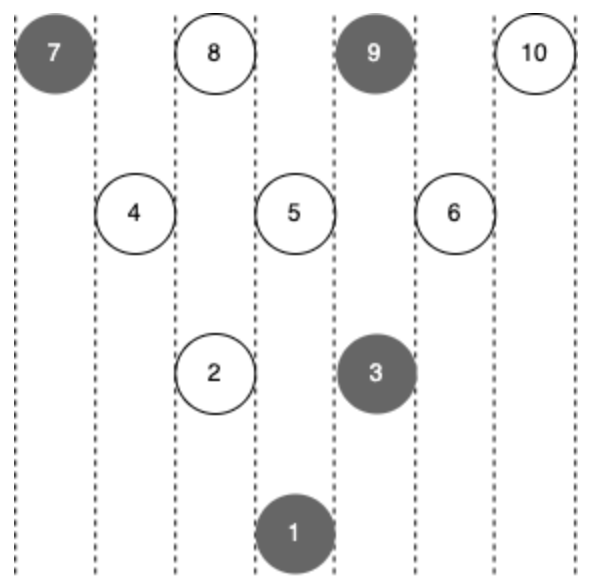
Між стовпчиком, що містить кегель 5, і стовпчиком, що містить кегель 6, знаходиться стовпець, що містить кеглі 3 і 9. Оскільки кеглі 3 і 9 обидва збиті, розміщення є розколом.
Приклад вхідних даних
0101110101Приклад вихідних даних
YesПриклад вхідних даних
0100101001Приклад вихідних даних
YesПриклад вхідних даних
0000100110Приклад вихідних даних
NoПриклад вхідних даних
1101110101Приклад вихідних даних
No
Коментарі