Вам задано ціле число \(N\) більше або дорівнює 2 і просте \(P\). Розглянемо граф \(G\) із \(2N\) вершинами та (\(3N-2\)) ребрами, показаними на малюнку нижче.

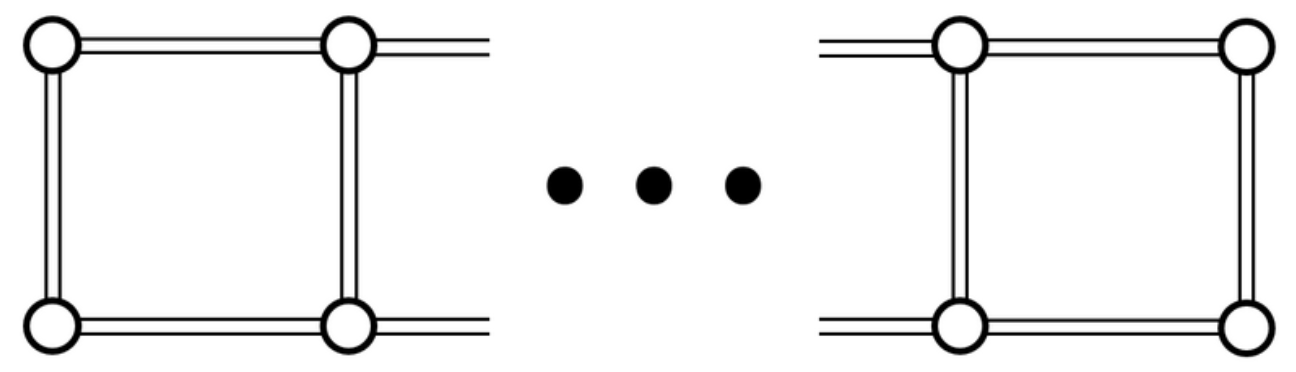
Точніше, ребра з’єднують вершини наступним чином, де вершини позначені як \(1, 2, \ldots, 2N\), а ребра пронумерованік \( 1, 2, \ldots, (3N- 2)\).

• Для кожного \(1 \leq i \leq N-1\) ребро \(i\) з’єднує вершину \(i\) та вершину \(i+1\).

• Для кожного \(1 \leq i \leq N-1\) ребро (\(N-1+i\)) сполучає вершину \(N+i\) та вершину \(N+i+1\).

• Для кожного \(1 \leq i \leq N\) ребро (\(2N-2+i\)) з’єднує вершину \(i\) та вершину \(N+i\).

Для кожного \(i=1,2,\ldots ,N-1\) розв’яжіть таку задачу.

Знайдіть кількість способів, за модулем \(P\), щоб видалити рівно \(i\) з \(3N-2\) ребер \(G\) так, щоб отриманий граф залишався зв’язним.

Обмеження

• \(2 \leq N \leq 3000\)
• 9 \times на 10^8 \leq P \leq 10^9~
• \(N\) — ціле число.
• \(P\) є простим числом.

Формат вхідних даних

Вхідний потік містить цілі числа \(N, P\)

Числа розділяються пропуском.

Формат вихідних даних

У вихідний потік виведіть \(N-1\) ціле число, \(i\)-те з яких є відповіддю на \(i=k\). Числа розділити пропусками.

Примітка

До прикладу 1:

У випадку \(N=3\) є 7 способів, як показано нижче, щоб видалити точно одне ребро, щоб отриманий граф залишався зв’язаним.

Існує 15 способів, як показано нижче, щоб видалити точно два ребра, щоб отриманий граф залишався зв’язаним.

Виводимо 7 і 15 у такому порядку (по модулю 998244353).

Приклад вхідних даних

3 998244353

Приклад вихідних даних

7 15

Приклад вхідних даних

16 999999937

Приклад вихідних даних

46 1016 14288 143044 1079816 6349672 29622112 110569766 330377828 784245480 453609503 38603306 44981526 314279703 408855776