Розмістіть \(B\) чорних тур і \(W\) білих тур на дошці з \(N\) горизонтальних рядків і \(M\) вертикальних стовпців. Розташування тур, що задовольняє всі наступні умови, називається хорошим розташуванням.

• Усі тури \(B+W\) розміщені на дошці.

• Щонайбільше одна тура розміщується в одному полі.

• Немає пари білої та чорної тур, які атакують одна одну. Тобто немає такої пари білої та чорної тури, щоб одна з них одним ходом могла досягти поля, на якому стоїть інша. Тут за один хід тура може досягти будь-якого поля, яке знаходиться на горизонтальній або вертикальній лінії від її поточної позиції та доступне, не перестрибуючи через іншу туру.

Скільки є хороших розміщень є?

Оскільки ця кількість може бути величезною, виведіть її за модулем 998244353.

Тури одного кольору не розрізняються.

Обмеження

• \(1 \leq N,M \leq 50\)

• \(1 \leq B,W \leq 2500\)

• \(B+W \leq N \times M\)

• Усі значення у вхідних даних є цілими числами.

Формат вхідних даних

Вхідний потік містить цілі числа \(N, M, B, W\)

Числа розділяються пропуском.

Формат вихідних даних

У вихідний потік виведіть шукану кількість розміщень

Примітка

До прикладу 1:

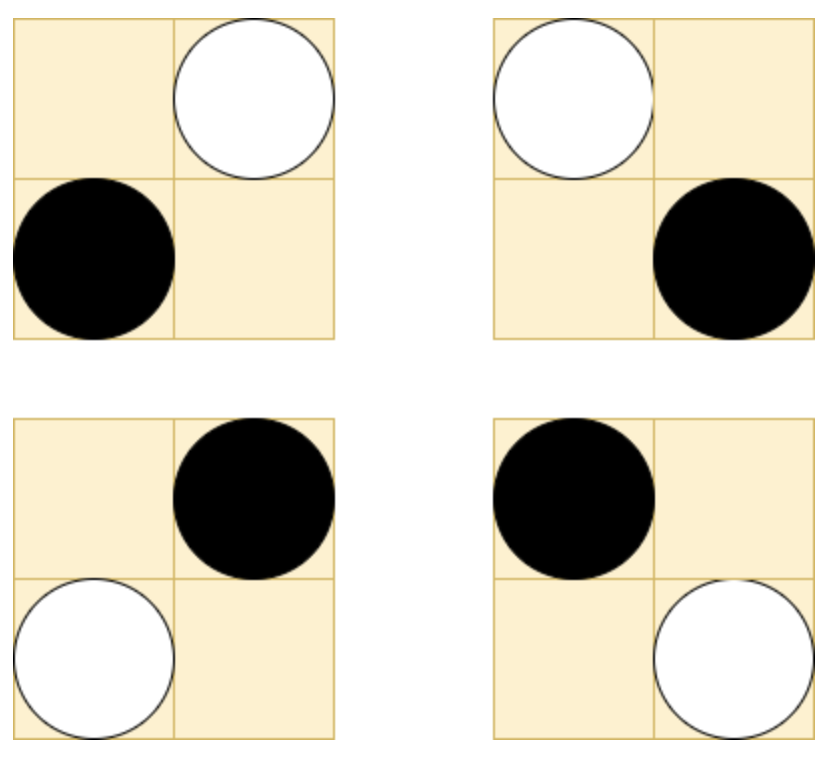
Приклад вхідних даних

2 2 1 1

Приклад вихідних даних

4

Приклад вхідних даних

1 2 1 1

Приклад вихідних даних

0

Приклад вхідних даних

40 40 30 30

Приклад вихідних даних

467620384