Існує нескінченна двовимірна сітка, і в клітині (\(r_1, c_1\)) знаходиться дракон. За один хід фігура дракон може перейти до однієї з клітин, які виділені кольором:

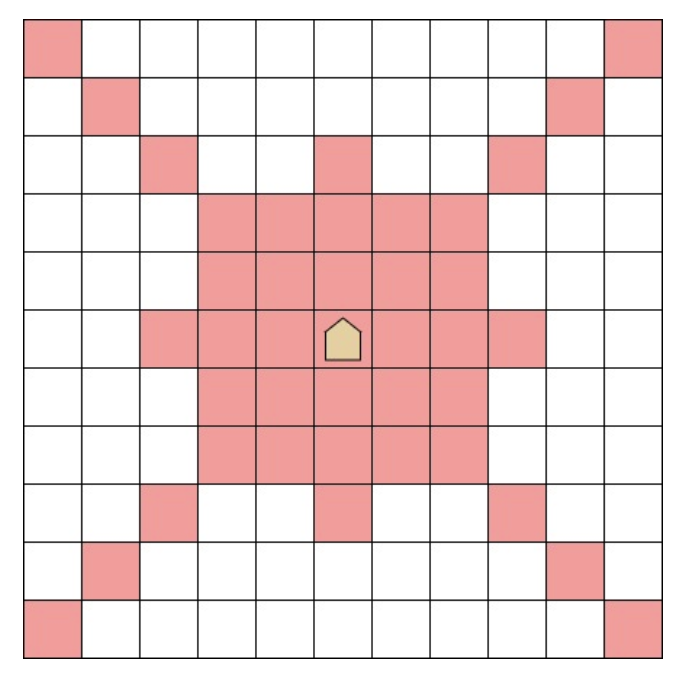
Більш формально, коли дракон знаходиться в клітині (\(a, b\)), то він може перейти в клітину (\(c, d\)) так, що виконується принаймні одне з наступного:

• \(a+b=c+d\)

• \(a−b=c−d\)

• \(∣a−c∣+∣b−d∣≤3\)

Знайдіть мінімальну кількість ходів, необхідну для досягнення драконом клітини (\(r_2, c_2\)).

Формат вхідних даних

Перший рядок містить цілі числа \(r_1, c_1\)

Наступний  рядок містить цілі числа \(r_2, c_2\) (\(1 \le r_1, c_1, r_2, c_2 \le 10^9\))

Числа у рядках розділяються пропуском.

Формат вихідних даних

У вихідний потік виведіть шукану кількість ходів.

Приклад вхідних даних

1 1
5 6

Приклад вихідних даних

2

Приклад вхідних даних

1 1
1 200001

Приклад вихідних даних

2

Приклад вхідних даних

2 3
998244353 998244853

Приклад вихідних даних

3