У нас є неорієнтований граф \(G\) з \(N\) вершинами, пронумерованими від 1 до \(N\) і \(N\) ребер:

• Для кожного \(i=1,2,...,N-1\) існує ребро між вершиною \(i\) та вершиною \(i+1\).

• Між вершиною \(X\) і вершиною \(Y\) є ребро.

Для кожного \(k=1,2,...,N-1\) розв’яжіть задачу нижче:

• Знайдіть кількість пар цілих чисел (\(i,j\)) (\(1 \leq i < j \leq N\)), таких, що найкоротша відстань між вершиною \(i\) та вершиною \(j\) у \(G\) є \(k\).

Формат вхідних даних

Вхідний потік містить цілі числа \(N, X, Y\) (\(3 \le N \le 2 \times 10^3\), \(1 \le X,Y \le N\), \(X+1 < Y\))

Формат вихідних даних

У вихідний потік виведіть  в окремому рядку для кожного \(k=1, 2, ..., N-1\) у такому порядку рядок, що містить відповідь задачі.

Примітка

До прикладу 1:

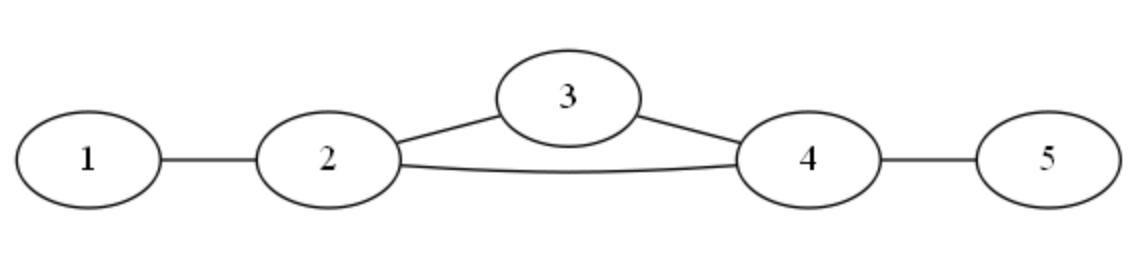
• Існує п'ять пар (\(i,j\)) (\(1 \leq i < j \leq N\)) таких, що найкоротша відстань між вершиною \(i\) та вершиною \(j\) дорівнює 1: (1 ,2),(2,3),(2,4),(3,4),(4,5).

• Є чотири пари (\(i,j\)) (\(1 \leq i < j \leq N\)), такі, що найкоротша відстань між вершиною \(i\) та вершиною \(j\) дорівнює 2: (1,3),(1,4),(2,5),(3,5).

• Існує одна пара (\(i,j\)) (\(1 \leq i < j \leq N\)), така що найкоротша відстань між вершиною \(i\) та вершиною \(j\) дорівнює 3: ((1,5).

• Немає пар (\(i,j\)) (\(1 \leq i < j \leq N\)), щоб найкоротша відстань між вершиною \(i\) та вершиною \(j\) дорівнювала 4.

Приклад вхідних даних

5 2 4

Приклад вихідних даних

5
4
1
0

Приклад вхідних даних

3 1 3

Приклад вихідних даних

3
0

Приклад вхідних даних

7 3 7

Приклад вихідних даних

7
8
4
2
0
0