Ось проста задача з графом: знайдіть найдешевший шлях від верхньо-середньої вершини до нижньо-середньої вершини в заданому триграфі. Триграф - це ациклічний граф із (\(2 \le N\)) рядків і рівно 3 стовпців. На відміну від звичайних графів, витрати в триграфі пов'язані з вершинами, а не з ребрами.

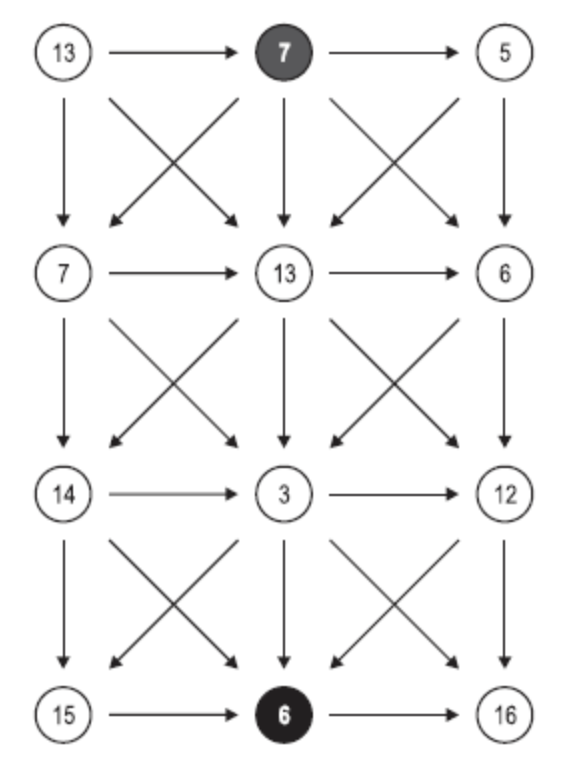
Отже, розглянувши приклад із \(N\) = 4, вартість спуску прямо зверху вниз уздовж середніх вершин становить 7 + 13 + 3 + 6 = 29. Розташування напрямних ребер у графі завжди таке ж, як проілюстровано на малюнку.

Формат вхідних даних

Вхідний потік містить декілька тестів. Кожен тест задається за допомогою \(N + 1\) рядків, де перший рядок містить ціле число \(N\) (\(2 \le N \le 10^5\)), що позначає кількість графі. Далі слідують \(N\) рядків, кожен із яких містить три цілі числа, що задають вартість вершин в \(i\)-му рядку, яка становить менше 1 000 000.

Після останнього тесту йде рядок з одним нулем.

Формат вихідних даних

У вихідний потік для кожного тесту в окремому рядку вивести мінімальну вартість описаношго шляху.

Приклад вхідних даних

4
13 7 5
7 13 6
14 3 12
15 6 16
0

Приклад вихідних даних

22