Дано дерево з \(N\) вершинами, пронумерованими від 1 до \(N\).

Корінь — це вершина \(1\), а \(i\)-е ребро \((1 \leq i \leq N - 1)\) з'єднує вершини \(a_i\) і \(b_i\). У кожній з вершин встановлений лічильник. Спочатку лічильники на всіх вершинах мають значення 0. Тепер будуть виконуватися такі операції \(Q\):

• Операція \(j\) \((1 \leq j \leq Q)\): збільшення на \(x_j\) лічильника на кожну вершину, що міститься в піддереві з коренем у вершині \(p_j\).

Знайдіть значення лічильника на кожній вершині після всіх операцій.

Формат вхідних даних

Перший рядок вхідного потоку містить цілі числа \(N, Q\) (\(2 \le N \le 2 \times 10^5\), \(1 \le Q \le 2 \times 10^5\)).

Наступні \(N-1\) рядків містять \(a_i, b_i\) (\(1 \le a_i < b_i \le N\)).

Далі ідуть \(Q\) рядків з парами цілих чисел \(p_j, x_j\) (\(1 \le p_j \le N\), \(1 \le x_j \le 10^4\))/

Числа у рядках розділяються пропуском.

Формат вихідних даних

У вихідний потік вивести значення лічильників на вершинах \(1, 2, \ldots, N\) після всіх операцій у такому ж порядку, з пропусками між ними.

Примітка

До прикладу 1:

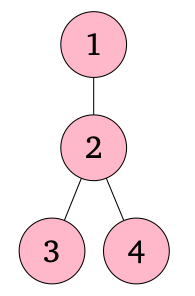
Кожна операція змінює значення лічильників у вершинах наступним чином:

• Операція 1: Збільшилися на 10 лічильники у кожній вершині, що містяться в піддереві з коренем у вершині 2, тобто у вершинах 2, 3, 4. Значення лічильників на вершинах 1, 2, 3, 4 тепер рівні 0, 10, 10, 10 відповідно.

• Операція 2: Збільшилися на 100 лічильники для кожної вершини, що містяться в піддереві з коренем у вершині 1, тобто у вершинах 1, 2, 3, 4. Значення лічильників на вершинах 1, 2, 3, 4 тепер становлять 100, 110, 110, 110 відповідно.

• Операція 3: Збільшилися на 1 лічильники для кожної вершини, що містяться в піддереві з коренем у вершині 3, тобто у вершині 3. Значення лічильників у вершині 1, 2, 3, 4 тепер становлять 100, 110, 111, 110 відповідно.

Приклад вхідних даних

4 3
1 2
2 3
2 4
2 10
1 100
3 1

Приклад вихідних даних

100 110 111 110

Приклад вхідних даних

6 2
1 2
1 3
2 4
3 6
2 5
1 10
1 10

Приклад вихідних даних

20 20 20 20 20 20