Існує дерево, яке має \(N\) вершин, які пронумеровані від 1 до \(N\). \(I\)-е ребро в цьому дереві з’єднує вершину \(a_i\) і вершину \(b_i\), а колір і довжина цього ребра є \(c_i\) і \(d_i\) відповідно.

Тут колір кожного ребра представлений цілим числом від 1 до \(N-1\) (включно).

Одне і те ж ціле число відповідає одному кольору, а різні цілі числа відповідають різним кольорам.

Дайте відповіді на такі \(Q\) запитів:

• Запит \(j\) (\(1 \leq j \leq Q\): -- припускаючи, що довжину кожного ребра, колір якого є \(x_j\) , змінено на \(y_j\) , знайдіть відстань між вершиною \(u_j\) і вершиною \(v_j\). (Зміни довжин ребер не впливають на наступні запити.)

Обмеження

• \(2 \le N \le 10^5\)
• \(1 \le Q \le 10^5\)
• \(1 \le a_i,b_i \le N\)
• \(1 \le c_i \le N−1\)
• \(1 \le d_i \le 10^4\)
• \(1 \le x_j \le N−1\)
• \(1 \le y_j \le 10^4\)
• \(1 \le u_j < v_j \le N\)

Граф є деревом.

Всі числа є цілими

Формат вхідних даних

Перший рядок вхідного потоку містить цілі числа \(N\), \(Q\).

Наступні \(N-1\) рядки містять цілі числа \(a_i, b_i, c_i, d_i\).

Далі ідуть \(Q\) рядків із запитами: цілі числа \(x_i, y_i, u_i, v_i\).

Числа у рядках розділяються пропуском. ​

Формат вихідних даних

У вихідний потік для кожного запиту в окремому рядку вивести відповідь.

Примітка

До прикладу 1:

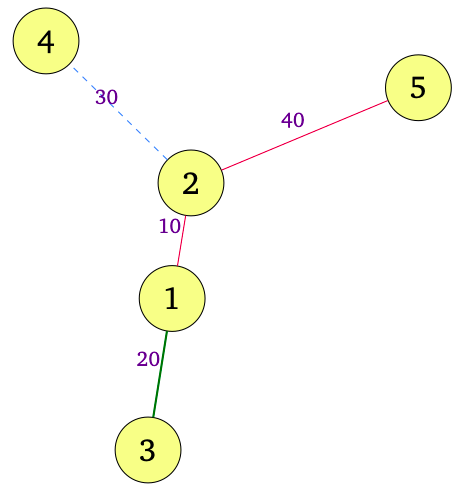
Тут ребра кольору 1 показані суцільними червоними лініями, ребра кольору 2 – жирною зеленою лінією, а ребра кольору 4 – блакитною пунктирною лінією.

• Запит 1: Припускаючи, що довжина кожного ребра, колір якого дорівнює 1, змінена на 100, відстань між вершиною 1 і вершиною 4 буде 100 + 30 = 130.

• Запит 2: Припускаючи, що довжину кожного ребра, колір якого дорівнює 1, змінено на 100, відстань між вершиною 1 і вершиною 5 буде 100 + 100 = 200.

• Запит 3: припускаючи, що довжину кожного ребра, колір якого дорівнює 3, змінено на 1000 (такого ребра немає), відстань між вершиною 3 і вершиною 4 дорівнює 20 + 10 + 30 = 60. Зверніть увагу, що ребра кольору 1 тепер мають оригінальну довжину.

Приклад вхідних даних

5 3
1 2 1 10
1 3 2 20
2 4 4 30
5 2 1 40
1 100 1 4
1 100 1 5
3 1000 3 4

Приклад вихідних даних

130
200
60