Вам дано дерево, яке має \(N\) вершин і \(N-1\) ребро. Вершини пронумеровані від 1 до \(N\), а \(i\)-е ребро з’єднує вершини \(a_i\) і \(b_i\).

У вас є \(K\) кольрів фарби. Для кожної вершини в дереві ви виберете один із \(K\) кольорів, щоб пофарбувати її,якщо виконується така умова:

• відстань між двома різними вершинами \(x\) і \(y\) менша або дорівнює двом, \(x\) і \(y\) мають різні кольори.

Відстань між двома вершинами \(x\) і \(y\) — це мінімальна кількість ребер, яку потрібно пройти, щоб дістатися з \(x\) до \(y\).

Скількома способами можна пофарбувати дерево? Знайдіть цю кількість за модулем 1000000007.

Формат вхідних даних

Перший рядок вхідного потоку містить цілі числа \(N,K\) (\(1 \le N,K \le 10^5\)).

Наступні \(N-1\) рядки містять пари цілих чисел \(a_i, b_i\) (\(1 \le a_i,b_i \le N\)).

Всі числа у рядках розділяються пропуском.

Формат вихідних даних

У вихідний потік виведіть шукану кількість способів.

Примітка

До прикладу 1:

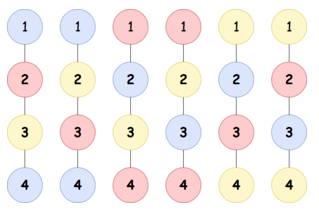
Приклад вхідних даних

4 3
1 2
2 3
3 4

Приклад вихідних даних

6

Приклад вхідних даних

5 4
1 2
1 3
1 4
4 5

Приклад вихідних даних

48

Приклад вхідних даних

16 22
12 1
3 1
4 16
7 12
6 2
2 15
5 16
14 16
10 11
3 10
3 13
8 6
16 8
9 12
4 3

Приклад вихідних даних

271414432