Для неорієнтованого дерева назвемо відстаню між вершинами \(u\) і \(v\) кількість ребер на шляху від \(u\) до \(v\). Діаметр дерева є максимальна серед відстаней між будь-якими двома вершинами. Будемо називати дерево гарним тоді і тільки тоді, коли його діаметр не більший \(K\).

Вам дано неорієнтоване дерево з \(N\) вершинами, пронумерованими від 1 до \(N\). Треба видалити нуль або більше вершин з дерева, щоб утворене дерево стало гарним. Коли вершина видаляється, всі ребра, що зустрічаються, також будуть видалені. Отриманий граф має бути зв'язним.

Знайдіть мінімальну кількість вершин, які потрібно видалити, щоб створити гарне дерево.

Формат вхідних даних

Перший рядок вхідного потоку місить два цілі числа \(N,K\) (\(2 \le N \le 2000\), \(1 \le K \le N-1\)).

Наступні \(N-1\) рядки містять ребра \(A_i\), \(B_i\) (\(1 \le A_i,B_i \le N\)).

Числа у рядках розділяються пропуском.

Формат вихідних даних

Вивести мінімальну кількість вершин, які потрібно видалити, щоб створити гарне дерево.

Примітка

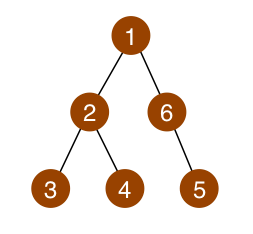
До прикладу 1:

Видалення вершин 5 і 6 дасть гарне дерево діаметром 2.

Приклад вхідних даних

6 2
1 2
3 2
4 2
1 6
5 6

Приклад вихідних даних

2

Приклад вхідних даних

6 5
1 2
3 2
4 2
1 6
5 6

Приклад вихідних даних

0