Три дзеркала довжиною \(N\) встановлені так, що вони утворюють рівносторонній трикутник. Нехай вершини трикутника будуть \(a, b, c\).

Усередині трикутника в точці \(p\) (\(|ap| = X\)) знаходиться лазер, який випускає чарівний промінь. Лазер випускає чарівний промінь у напрямку \(ac\) паралельно cтороні \(bc\).

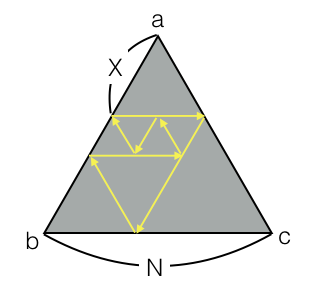
Чарівний промінь рухається по прямій лінії і буде відбиватися від дзеркал так само, як і «звичайне» світло. Хоча є одна суттєва відмінність: цей промінь також буде відображатися власною траєкторією, ніби це дзеркало! Коли чарівний проміньь повернеться у вихідну точку, то він поглиннається.

Можна показати, що промінь з часом повертається у вихідну точку і поглинається незалежно від значень \(N\) і \(X\). Знайдіть загальну довжину траєкторії променя.

Формат вхідних даних

Вхідний потік містить два цілі числа \(N, X\) (\(2 \le N \le 10^{12}\), \(1 \le X \le N-1\)), які розділяються пропуском.

Формат вихідних даних

У вихідний потік виведіть загальну довжину траєкторії променя.

Пояснення

До прикладу вхідних даних (малюнок відповідає цьому прикладу, точка \(p\) не позначена):

2 + 3 + 2 + 2 + 1 + 1 + 1 = 12

Приклад вхідних даних

5 2

Приклад вихідних даних

12