У Флатландії протікає багата рибою річка Великий Флат. Багато років тому річка була поділена між рибальськими підприємствами, кожне з яких отримало безперервний відрізок річки. При цьому \(𝑖\) -е підприємство, якщо розглядати їх по порядку, починаючи від витоку, спочатку одержало відрізок річки завдовжки \(𝑎_𝑖\).

З того часу з рибальськими підприємствами у Флатландії раз відбувалися різні події. Кожна з подій була однією з двох типів: банкрутство деякого підприємства чи поділ деякого підприємства на два.

За деяких подій відрізок річки, що належить підприємству, з яким ця подія відбувається, поділяється на дві частини. Кожен такий відрізок має довжину більшу або рівну 2. Розподіл відбувається за таким правилом. Якщо відрізок має парну довжину, він ділиться на дві рівні частини. Інакше він ділиться на дві частини, довжини яких різняться рівно на одиницю, при цьому частина, що ближче до початку річки, має меншу довжину.

При банкрутстві підприємства відбувається таке. Відрізок річки, що належав підприємству, що збанкрутував, переходить до його сусідів. Якщо в збанкрутілого підприємства один сусід, то цьому сусіду цілком передається відрізок річки збанкрутілого підприємства. Якщо ж сусідів двоє, то відрізок річки ділиться на дві частини описаним вище способом, після чого кожен із сусідів приєднує до свого відрізку найближчу до нього частину.

При поділі підприємства відрізок річки, що належав підприємству, що поділяється, завжди ділиться на дві частини описаним вище способом. Підприємство, що розділилося, ліквідується, і утворюються два нових підприємства. Таким чином, після кожної події кожне підприємство має певний відрізок річки.

Міністерство фінансів Флатландії пропонує запровадити податок на рибальські підприємства, пропорційний квадрату довжини відрізка річки, що належить відповідному підприємству. Щоб проаналізувати, як працюватиме цей податок, міністр хоче за наявними даними дізнатися, як змінювалася величина, що дорівнює сумі квадратів довжин відрізків річки, що належать підприємствам, після кожної події, що відбулася.

Потрібно написати програму, яка за заданим початковим поділом річки між підприємствами та списком подій, що відбувалися з підприємствами, визначить, чому дорівнює сума квадратів довжин відрізків річки, що належать підприємствам, у початковий момент часу та після кожної події.

Формат вхідних даних

Перший рядок вхідного файлу містить два цілих числа: \(𝑛\) і \(𝑝\) — вихідна кількість підприємств (\(2 ≤ 𝑛 ≤ 100 000\)) та номер підзавдання (\(0 ≤ 𝑝 ≤ 4\)).

Другий рядок вхідного файлу містить \(𝑛\) цілих чисел \(𝑎_1 , 𝑎_2 , …, 𝑎_𝑛\) - довжини вихідних відрізків річки.

Третій рядок вхідного файлу містить ціле число \(𝑘\) - кількість подій, що відбувалися з підприємствами (\(1 ≤ 𝑘 ≤ 100 000\)).

Наступні рядків містять опис подій, - рядок містить два цілих числа: \(𝑒_𝑖\) і \(𝑣_𝑖\) - тип події і номер підприємства, з яким воно сталося. Значення \(𝑒_𝑖 = 1\) означає, що підприємство, яке після всіх попередніх подій є \(𝑣_𝑖\) -м по порядку, якщо рахувати з одиниці від витоку річки, збанкрутувало, а значення \(𝑒_𝑖 = 2\) означає, що це підприємство розділилося на два.

Гарантується, що значення \(𝑣_𝑖\) не перевищує поточну кількість підприємств. Гарантується, що якщо відрізок підприємства при банкрутстві чи розподілі потрібно поділити на дві частини, то він має довжину більшу або рівну 2. Гарантується, що якщо на річці залишилося єдине підприємство, воно не банкрутується.

Формат вихідних даних

Вихідний файл повинен містити (\(𝑘+1\)) цілих чисел, по одному в рядку.

Перший рядок повинен містити вихідну суму квадратів довжин відрізків річки, а кожен із наступних рядків — суму квадратів довжин відрізків річки після чергової події.

Пояснення

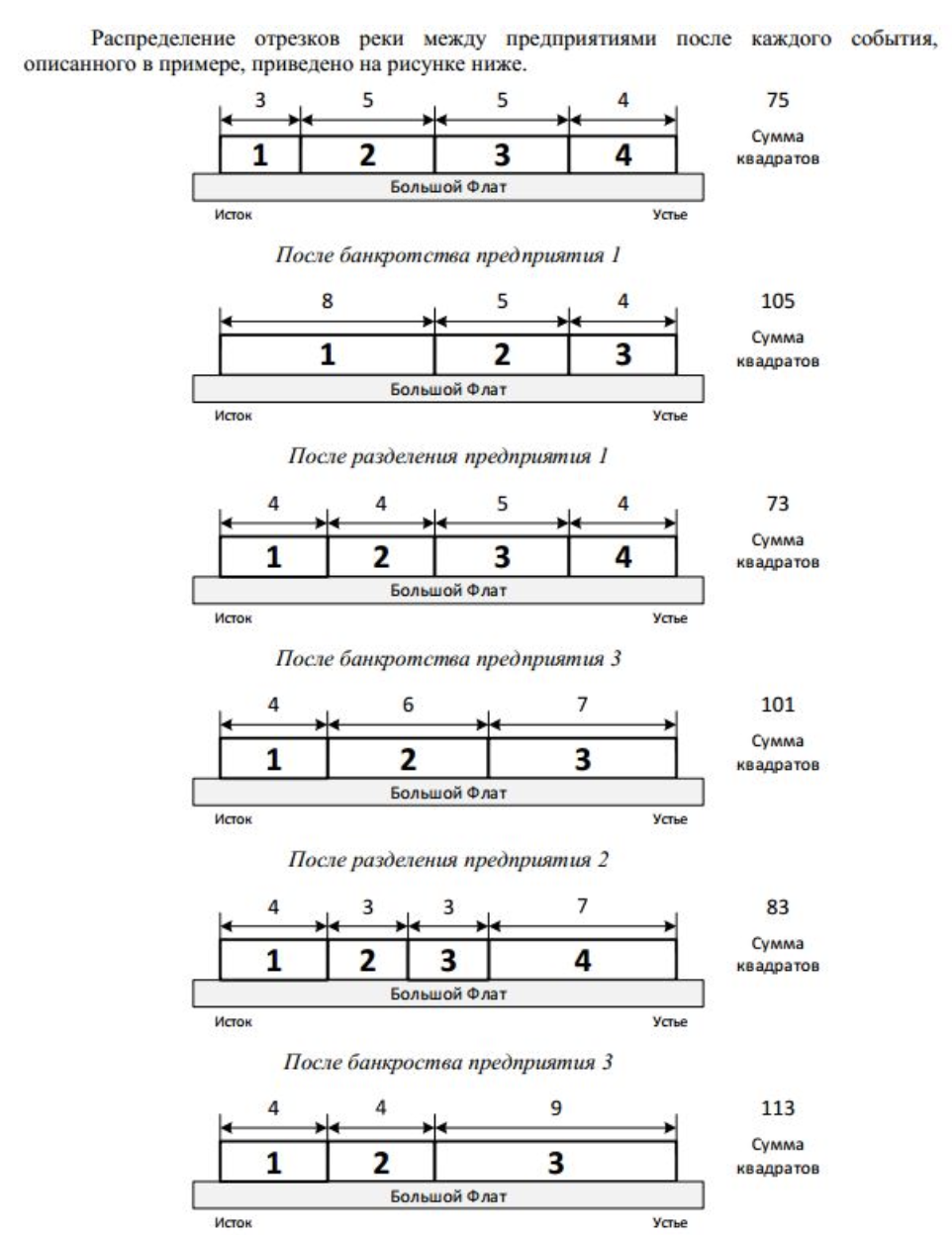
Система оцінки та опис підзадач

У цьому завданні чотири підзадачі. Бали за кожне підзавдання нараховуються лише у випадку, якщо всі тести для цієї підзадачі успішно пройдені.

Увага! Тест із прикладу не підходить під обмеження підзавдання 3. Проте, вирішення завдання приймається на перевірку тільки в тому випадку, якщо воно виводить правильну відповідь на тесті з прикладу, навіть якщо учасник претендує на правильне рішення лише цього підзавдання.

У першому рядку кожного тесту після числа \(n\) вказано номер підзадачі, для тесту з прикладу вказано число 0, у тестах першого підзадачі вказано число 1, і т. д.

• Підзавдання 1 (30 балів) \(2 ≤ 𝑛 ≤ 100\), \(1 ≤ 𝑘 ≤ 100\) , \(1 ≤ 𝑎_𝑖 ≤ 100\), \(𝑝 = 1\)
• Підзавдання 2 (30 балів) \(2 ≤ 𝑛 ≤ 100 000\), \(1 ≤ 𝑘 ≤ 100 000\), \(1 ≤ 𝑎_𝑖 ≤ 10^4\), \(p=2\) Для всіх \(i\) від 1 до \(k-1\) виконано умову : \(|𝑣_𝑖– 𝑣_{𝑖+1}| ≤ 10\)
• Підзавдання 3 (20 балів) \(2 ≤ 𝑛 ≤ 100 000\), \(1 ≤ 𝑘 ≤ 100 000\), \(1 ≤ 𝑎_𝑖 ≤ 10^4\), \(𝑝 = 3\) Усі події мають тип \(𝑒_𝑖= 1\) (немає поділів підприємств, лише банкрутства).
• Підзавдання 4 (20 балів) \(2 ≤ 𝑛 ≤ 100 000\), \(1 ≤ 𝑘 ≤ 100 000\), \(1 ≤ 𝑎_𝑖 ≤ 10^4\), \(𝑝 = 4\)

Приклад вхідних даних

4 0
3 5 5 4
5
1 1
2 1
1 3
2 2
1 3

Приклад вихідних даних

75
105
73
101
83
113