Як і в звичайному тетрісі, поле в грі Strategy Tetris є "склянкою" шириною в \(W\) клітин (\(1 \le W \le 10^9\)) і нескінченної висоти. У цю склянку падають зверху \(N\) фігурок (\(1 \le N \le 100000\)). \(i\)-я фігурка являє собою прямокутник шириною \(W_i\) клітин і висотою в одну клітину; найлівіша клітина фігурки має абсцису \(a_i\) (\(1 \le a_i \le W–W_i+1\)). Фігурки падають за звичайними правилами: якщо при падінні фігурка хоча б однією своєю клітиною лягає на якусь фігурку, що вже впала, то її рух припиняється.

На відміну від звичайного тетрісу, гравець не має можливості обертати фігурки або зміщувати їх по горизонталі в процесі падіння - звичайно, це довелося б робити швидко і не було б часу серйозно подумати над стратегією. Єдине, що він може - це вибрати порядок, в якому ці \(N\) фігурок впадуть у склянку (кожна по одному разу).

Ваше завдання — допомогти йому вибрати такий порядок, при якому висота конструкції, що утворилася в результаті падіння, була б якнайменше. (На відміну від звичайного тетрісу, повністю заповнена фігурками горизонталь нікуди не зникає).

Нижче наведено приклад заповнення склянки фігурками з прикладу вхідних даних (порядок заповнення відповідає вихідному файлу, наведеному в прикладі).

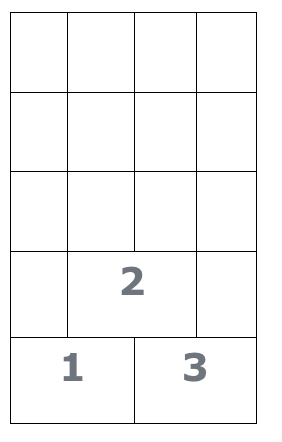
Формат вхідних даних

У першому рядку вхідного файлу записані числа \(N\) і \(W\), а в наступних \(N\) рядках — пари чисел \(a_i\) і \(W_i\).

Формат вихідних даних

Виведіть у вихідний файл мінімальну можливу висоту конструкції, а потім послідовність номерів фігурок, що приводить до цієї висоти. Фігурки нумеруються натуральними числами від 1 до \(N\) у порядку, в якому вони вказані у вхідних даних. Якщо можливих варіантів є кілька, виведіть будь-який з них.

Приклад вхідних даних

3 4
1 2
2 2
3 2

Приклад вихідних даних

2
3 1 2