У розважальному центрі Е-міста було встановлено ігровий автомат нового покоління. В автомат можна кинути монету і стежити за її просуванням зверху вниз по лабіринту, що розгалужується, з трубок. У лабіринті є \(n\) вузлів, пронумерованих числами від 1 до \(𝑛\) . При киданні монета потрапляє у перший вузол. Кожен вузол лабіринту, крім першого, має одну трубку, що входить зверху, по якій монета може в нього потрапити. З кожного вузла виходить не більше двох трубок, що йдуть вниз, одна з яких веде ліворуч, а інша праворуч. Кожна трубка має деяку ширину. Монета провалюється в ширшу трубку, а у разі рівності ширини трубок – у ліву.

Після проходження монети по трубці ширина цієї трубки зменшується на 1. Монета не може пройти по трубці ширини 0. Якщо монета досягла вузла, з якого вона не може далі рухатися вниз, автомат зупиняється і чекає, коли в нього кинуть наступну монету.

На початку в кожному вузлі лабіринту знаходиться по іграшці. Коли монета потрапляє у вузол вперше, іграшка, що у цьому вузлі, дістається гравцю, який кинув цю монету.

Степанові сподобалася іграшка, яка знаходиться у вузлі з номером \(𝑣\).

Потрібно написати програму, яка визначає скільки монет повинен кинути в автомат Степан, щоб отримати іграшку з вузла \(𝑣\) .

Формат вхідних даних

У першому рядку вхідного файлу міститься число \(𝑛\) — кількість вузлів у лабіринті.

У наступних \(n\) рядках задані описи всіх вузлів, в \(k\)-у з цих рядків описаний вузол з номером \(k\) .

Опис \(k\)-го вузла складається з чотирьох цілих чисел: \(𝑎_𝑘 , 𝑢_𝑘 , 𝑏_𝑘 , 𝑤_𝑘 \). Якщо з \(k\)-го вузла виходить ліва трубка, то \(𝑎_𝑘\) - номер вузла, до якого вона веде (\(𝑘 < 𝑎_𝑘 <= 𝑛\) ), а \(𝑢_𝑘\) - її ширина. Якщо лівої трубки немає, то \(𝑎_𝑘 = 𝑢_𝑘 = 0\). Якщо з \(k\)-го вузла виходить права трубка, то \(b_k\) номер вузла, в який вона веде (\(k < b_k \le n\)), а \(w_k\) її ширина. Якщо правої трубки немає, то \(𝑏_𝑘 = 𝑤_𝑘 = 0\).

В останньому рядку задано ціле число \(𝑣\) (\(1 \le 𝑣 \le 𝑛 \)) — номер вузла, в якому знаходиться іграшка, яка сподобалася Степану.

Гарантується, що до всіх вузлів, крім першого, входить рівно одна трубка

Формат вихідних даних

Вихідний файл повинен містити одне число — кількість монет, яку необхідно кинути в автомат Степану, щоб отримати іграшку, яка знаходиться у вузлі \(𝑣\) . Якщо вибрати іграшку неможливо, виведіть число −1.

Система оцінки

Це завдання містить дві підзадачі. Для оцінки кожного підзавдання використовується своя група тестів. Бали за підзавдання нараховуються тільки в тому випадку, якщо всі тести цієї групи пройдені.

• Підзавдання 1 \(1 \le 𝑛 \le 100\) \(1 \le 𝑢_𝑘\); \(𝑤_𝑘 \le 300\) Підзавдання оцінюється в 50 балів.
• Підзавдання 2 \(1 \le 𝑛 \le 10^5\) \(1 \le 𝑢_𝑘; 𝑤_𝑘 \le 10^9\) Підзавдання оцінюється в 50 балів.

Пояснення

У першому прикладі перша монета пройде лабіринт наступним шляхом, і гравець отримає іграшки з вершин 1, 3 і 4:

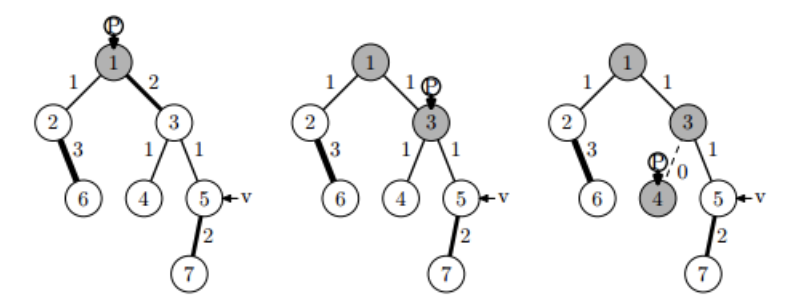
Друга монета пройде лабіринт наступним шляхом, і гравець отримає іграшки з вершин 2 і 6:

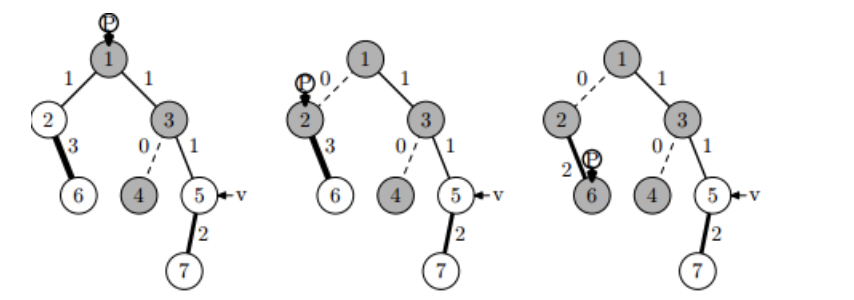
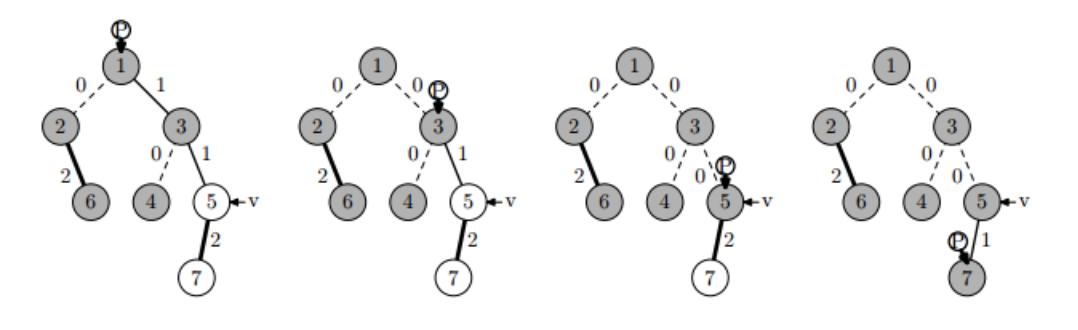
Третя монета пройде лабіринт наступним шляхом шляху, і гравець отримає іграшки з вершин 5 та 7:

Приклад вхідних даних

7
2 1 3 2
0 0 6 3
4 1 5 1
0 0 0 0
7 2 0 0
0 0 0 0
0 0 0 0
5

Приклад вихідних даних

3

Приклад вхідних даних

4
0 0 2 1
4 1 3 1
0 0 0 0
0 0 0 0
3

Приклад вихідних даних

-1