Антон – великий любитель комп'ютерних ігор. Нещодавно вийшла нова гра Heroes of Keyboard and Mouse, і він, звичайно ж, відразу її купив і встановив на свій комп'ютер. Ця гра належить до жанру квестів, і тому її проходження зводиться до послідовного виконання низки завдань (квестів).

Один із квестів, над яким Антон б'ється вже не перший день у тому, що потрібно відкрити замок. Замок складається з \(n\) шестерень, що стоять в ряд - \(i\)-а з шестерень має \(s_i\) зубців, на кожному з яких написано число від 0 до \(s_i-1\) Перша шестерня зачеплена тільки з другою, друга зачеплена з першою і третьою, третя - з другої і четвертої, ..., \((𝑛−1)\) -а - з \((𝑛−2)\) -ю і \(𝑛\) -ю, \(𝑛\) -а тільки з \((𝑛−1)\) -ю.

На замку є \(n\) віконець і \(n\) ручок - в \(i\)-е вікно можна бачити число, написане на одному із зубців \(𝑖\) -ої шестерні, а за допомогою \(𝑖\) -ої ручки можна повертати \(𝑖\) -у шестерню. При цьому числа на шестернях розташовані таким чином, що якщо до повороту \(𝑖\)-ої з них за годинниковою стрілкою на один поділку в \(𝑖\)-му вікні було видно число \(𝑥\), то після повороту буде видно число \((𝑥+1)\) mod \(𝑠_𝑖\). Аналогічно, після повороту проти годинникової стрілки на одну поділку замість числа \(𝑥\) буде видно число \((𝑥−1+𝑠_𝑖)\) mod \(𝑠_𝑖 \). Зрозуміло, якщо шестерню повернути за годинниковою стрілкою, то безпосередньо зачеплені з нею шестерні повернуться проти годинникової стрілки, і навпаки, якщо шестерню повернути проти годинникової стрілки, то вони повернуться за годинниковою стрілкою. Зліва на рис.1 показано положення шестерні до повороту першої з них за годинниковою стрілкою, праворуч на рис. 1 показано положення шестерні після зазначеного повороту. Товстішими лініями намальований той зубець шестерні, число на якому видно у відповідне віконце замку.

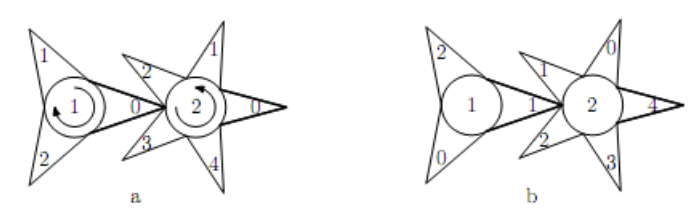
рис.1

Спочатку замок перебуває в стані, в якому у \(i\)-е віконце видно число \(a_i\). Для того, щоб його відкрити, необхідно перевести його в стан, в якому в вікно видно число \(𝑏_𝑖\) .

За допомогою \(i\)-ї ручки можна повертати \(i\)-у шестерню. Зрозуміло, якщо повернути \(i\)-у шестерню, то почнуть рухатися і всі шестерні, з якими вона з'єднана - безпосередньо або через інші шестерні. Поворот будь-якої шестерні на один поділ займає одну секунду. Крім цього, якщо \(i\)-у шестерня знаходиться в такому стані, що в \(i\)-е вікно видно число \(𝑏_𝑖\) (тобто, вона знаходиться в положенні, що відповідає необхідному стану замку), то її можна втиснути, натиснувши на її ручку. В результаті цього \(i\)-а шестерня перестає бути з'єднаною з (\(i -1\)) -ю і (\(i+1\)) -ю (якщо, звичайно, вони існують). Вдавлена шестірня залишається в такому стані назавжди. На те, щоб натиснути на ручку і вдавити шестірню потрібно \(𝑘\) секунд. На рис. 2 зліва показано положення шестерні до вдавлювання другої з них, а праворуч - після вдавлювання і після повороту першої за годинниковою стрілкою, а третьої - проти. Зазначимо, що після вдавлювання другої шестерні перша і третя обертаються незалежно одна від одної.

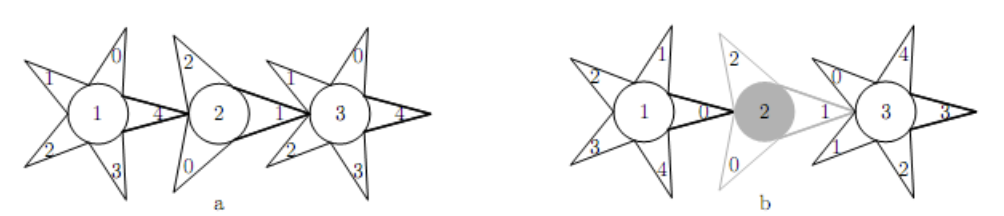
Рис.2

Для того, щоб виконати квест, Антону необхідно відкрити замок якнайшвидше. Напишіть програму, яка за описом замку, його початкового стану та необхідного стану обчислить мінімальний час, за який Антон може відкрити замок.

Формат вхідних даних

Перший рядок містить два цілих числа: \(𝑛\) і \(𝑘\) (\(1≤𝑛≤25\) , \(1≤𝑘≤100 \)).

Другий рядок містить \(𝑛\) чисел: \(𝑠_1 , 𝑠_2 , ..., 𝑠_𝑛\) - розміри шестерень. Всі \(𝑠_𝑖\) - цілі числа від 3 до 10.

Третій рядок містить \(𝑛\) цілих чисел \(𝑎_1 , 𝑎_2 , ..., 𝑎_𝑛\) - початкові положення шестерень (для всіх \(𝑎_𝑖\) виконуються нерівності \(0 \le a_i \le s_i\)).

Четвертий рядок містить \(𝑛\) цілих чисел \(𝑏_1 , 𝑏_2 , ..., 𝑏_𝑛\) - необхідні положення шестерень (для всіх \(𝑏_𝑖\) виконуються нерівності \(0≤𝑏_𝑖<𝑠_i\)).

Формат вихідних даних

Виведіть мінімальну кількість часу, яка потрібна для того, щоб відкрити замок.

Приклад вхідних даних

2 2
3 5
0 0
1 1

Приклад вихідних даних

4

Приклад вхідних даних

3 2
3 3 3
0 0 0
1 1 1

Приклад вихідних даних

5