Група вчених працює у міжнародній науковій лабораторії, яка займається дослідженнями поведінки елементарних частинок в установці для експериментів «Великий лінійний колайдер» (ВЛК). Установка ВЛК є прямою, в деяких точках якої розміщуються частинки, які можуть переміщатися вздовж прямої.

У черговому експерименті у ВЛК розміщуються \(n\) частинок, кожна з яких є або відʼємною зарядженою частинкою - \(е^-\) , або додатно зарядженою частинкою - позитрон \(е^+\) . В експерименті 𝑖-я частка вихідно розміщується в точці з координатою 𝑥𝑖. Після початку експерименту в результаті роботи ВЛК частинки почнуть переміщатися в різні сторони вздовж прямої: \(е^-\) частинки переміщаються за зменшенням координати, а \(е^+\) частинки - за напрямом збільшення координати. Абсолютні величини швидкостей всіх частинок однакові й рівні 1.

Якщо процесі переміщення частинки \(е^–\) і \(е^+\) виявляються в одній точці, то всі вони взаємодіють і обидві зникають, при цьому вони не впливають більше на поведінку інших частинок.

Вчені вибрали \(𝑚\) різних моментів часу \(𝑡_1,𝑡_2,…,𝑡_𝑚\) , для кожного з яких їх цікавить, скільки частинок знаходиться в ВЛК безпосередньо після кожного з цих моментів часу. Відлік часу починається з моменту 0, коли частмнки починають рухатися. Частинки, що зникли в результаті взаємодії в момент часу \(t_j\), не повинні враховуватися при підрахунку кількості частинок для цього моменту часу.

Потрібно написати програму, яка за описом розташування та типів частинок, а також за заданим моментам часу визначає для кожного з моментів кількість частинок, яка буде знаходитися в ВЛК безпосередньо після цього моменту.

Формат вхідних даних

Перший рядок містить число \(𝑛\) — кількість частинок (\(1≤𝑛≤200000\)).

Наступні рядків описують частинки наступним чином: кожен рядок містить по два цілих числа \(x_i\) і \(v_i\) - координату \(i\)-ї частинки та її тип відповідно. (\(-10^9 \le x_1 < x_2< ... < x_n \le 10^9\), \(v_i=1\) або -1). Частинка \(е^-\) описується значенням \(𝑣_𝑖=-1\) , а частинка \(е^+\) описується значенням \(𝑣_𝑖 = 1\) .

Наступний рядок містить ціле число \(𝑚\) - кількість моментів часу, які вибрали вчені (\(1≤𝑚≤200000\)).

Останній рядок містить \(𝑚\) цілих чисел: \(𝑡_1,𝑡_2,…,𝑡_𝑚\) (\(0…𝑡_1<𝑡_2<⋯<𝑡𝑚≤10^9 \)).

Формат вихідних даних

Для кожного моменту часу потрібно вивести одне число: кількість частинок у ВЛК безпосередньо після цього моменту.

Пояснення

У наведеному прикладі в початковий момент у ВЛК знаходяться 4 частинки: частинка \(е^+\) в точці -1, частинка \(е^-\) в точці 0, частинка \(е^+\) в точці 1 і частинка \(е^-\) в точці 5.

У момент часу 0.5 перша частинка \(е^+\) і перша частинка \(е^-\) зіштовхуються в точці з координатою -0.5 і зникають. У момент часу 1 дві частинки, що залишилися, знаходяться в точках з координатами 2 і 4, відповідно. На момент часу 2 вони стикаються в точці 3 і зникають. Більше у ВЛК частинок немає

Оцінювання

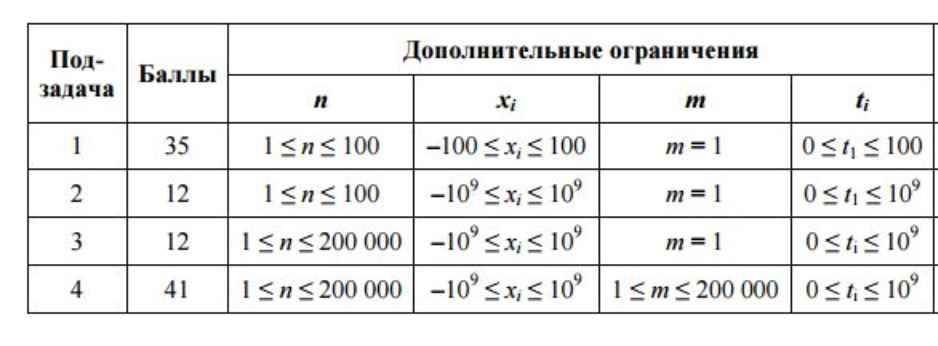
Приклад вхідних даних

4
-1 1
0 -1
1 1
5 -1
4
0 1 2 3

Приклад вихідних даних

4
2
0
0