У процесі ремонту в Лабораторії Інформаційних Технологій будівельникам необхідно замінити пошкоджені плитки для підлоги в коридорі лабораторії, який має розмір \(2 × 𝑛\) метрів. У розпорядженні будівельників є необмежений запас плиток двох розмірів: \(1 × 2\) метри та \(1 × 1\) метр. При цьому плитки розміром \(1 × 2\) метри перед укладанням дозволяється повертати на 90 градусів і розміщувати вздовж і поперек коридору.

Будівельники вже розпочали ремонт і уклали в деяких місцях підлоги коридору плитки розміром \(1 × 1\). Для завершення ремонту виконробу необхідно підготувати план подальших робіт. Для цього йому треба вирішити, як укласти плитки на місця, де вони ще не укладені. Це можна зробити різними способами і виконроб хоче перебрати всі варіанти і вибрати найвдаліший. Перед тим як це зробити, виконроб хоче знати, скільки варіантів йому доведеться розглянути. Це число потрібно знайти за модулем \(10^9+7\).

Потрібно написати програму, яка за заданою довжиною коридору і розташуванням плиток, які вже укладені, визначає кількість способів укладання плиток на місця, що залишилися.

Відповідь необхідно вивести за модулем \(10^9+7\).

Формат вхідних даних

Перший рядок вхідного файлу містить два цілих числа: \(𝑛\) - довжину коридору і \(𝑘\) - кількість вже укладених одиничних плиток (\(1 ≤ 𝑛 ≤ 100 000\), \(0 ≤ 𝑘 < 2n\)

Наступні \(𝑘\) рядків містять по два цілих числа \(𝑥_𝑖\) і \(𝑦_𝑖\) , які задають позиції вже покладених одиничних плиток, \(i\) плитка укладена на \(x_i\) метрі коридору в \(y_i\) ряді (\(1 \le x_i \le n\), \(1 \le 𝑦_𝑖 ≤ 2\))

Формат вихідних даних

Вихідний файл повинен містити одне ціле число — кількість способів укладання плиток у коридорі, взята за модулем \(10^9+7\).

Пояснення до прикладів

Всі способи укладання плиток для першого прикладу:

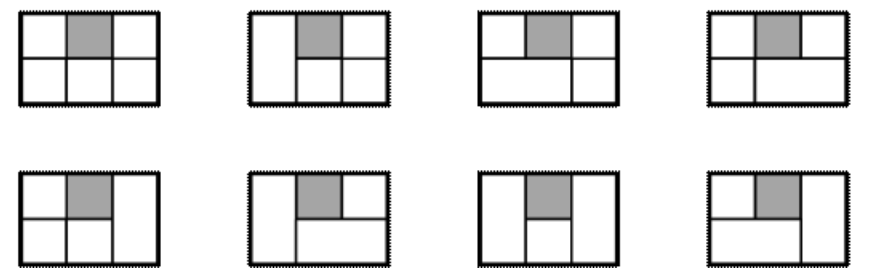
Всі способи укладання плиток для третього прикладу (уже укладена плитка відзначена сірим кольором):

Система оцінки та опис підзавдань

• Підзавдання 1 (20 балів) \(1 ≤ 𝑛 ≤ 8\), \(𝑘 = 0\)
• Підзавдання 2 (20 балів) \(1 ≤ 𝑛 ≤ 1000, 𝑘 = 0\)
• Підзавдання 3 (20 балів) \(1 ≤ 𝑛 ≤ 100 000, 𝑘 = 0\)
• Підзавдання 4 (40 балів) \(1 ≤ 𝑛 ≤ 100 000, 1 ≤ 𝑘 ≤ 2𝑛\)

Бали за підзавдання нараховуються лише у випадку, якщо всі тести підзадачі пройдені.

Приклад вхідних даних

2 0

Приклад вихідних даних

7

Приклад вхідних даних

3 0

Приклад вихідних даних

22

Приклад вхідних даних

3 1
2 1

Приклад вихідних даних

8