Широке поширення в стандартних бібліотеках багатьох мов програмування набула реалізація збалансованих дерев на основі так званих червоно-чорних дерев. У цьому завдання вам пропонується порахувати кількість червоно-чорних дерев заданої форми.

Нагадаємо, що двійковим деревом називається набір вершин, організованих у вигляді дерева. Кожна вершина має трохи більше двох дітей, одне із яких називається лівим, а інший – правим. Як ліва, так і права дитина, а також обидва можуть бути відсутніми.

Якщо вершина \(Y\) - дитина вершини \(X\), то кажуть, що вершина \(X\) є батьком вершини \(Y\). У кожної вершини дерева, крім однієї, є рівно один з батьків. Єдина вершина, яка не має батька, називається коренем дерева.

З'єднаємо кожну вершину, крім кореня, із її батьком. Зауважимо, що для кожної вершини існує рівно один шлях, що веде до неї від кореня.

Двійкове дерево називається червоно-чорним, якщо кожна його вершина розфарбована в червоний або чорний колір, причому виконуються такі умови:

• якщо вершина червона, то її батько – чорний;
• кількість чорних вершин на шляху від кореня до будь-якої вершини, у якої відсутня хоча б одна дитина, така сама.

Приклади двійкового дерева, вершини якого розфарбовані у два кольори, наведено на малюнку.

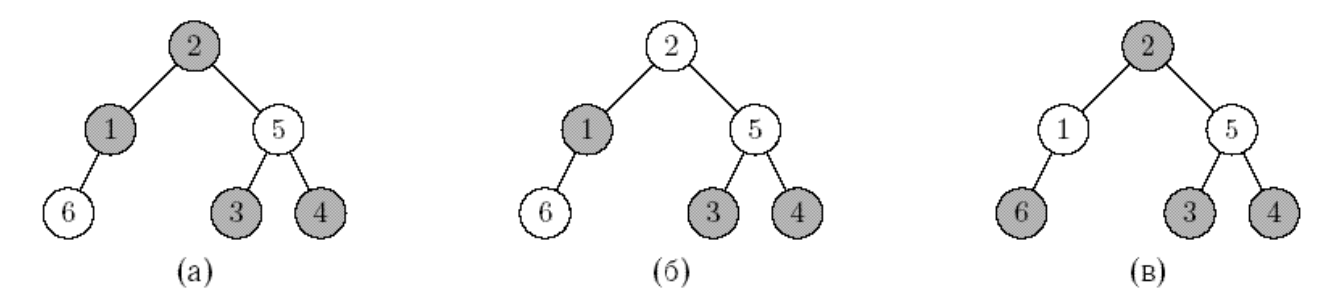
Якщо вважати зафарбовані вершини чорними, а незафарбовані – червоними, то дерево на малюнку (а) є червоно-чорним деревом, а дерева на малюнках (б) і (в) – ні. Для дерева на малюнку (б) порушується перша властивість – у червоної вершини 5 батько 2 також червоний, а в дереві на малюнку (в) порушується друга властивість – на шляху від кореня до вершини одна чорна вершина, а, наприклад, на шляху від кореня до вершини 3 – дві.

Для заданого двійкового дерева підрахуйте кількість способів розфарбувати його вершини у чорний та червоний колір так, щоб воно стало червоно-чорним деревом.

Формат вхідних даних

У першому рядку вводиться число \(n\) – кількість вершин у дереві ( \(1 \le n \le 1000\))

Нехай вершини дерева пронумеровані числами від 1 до \(n\). Наступні \(n\) рядків містять по два числа – для кожної вершини задані номери її лівої та правої дитини. Якщо один із дітей відсутній, то замість його номера записано нуль.

Гарантується, що вхідні дані коректні, тобто набір чисел, що вводяться, дійсно задає двійкове дерево.

Формат вихідних даних

Виведіть одне число – кількість способів розфарбувати вершини заданого двійкового дерева у червоний та чорний кольори так, щоб воно стало червоно-чорним деревом.

Пояснення до прикладу

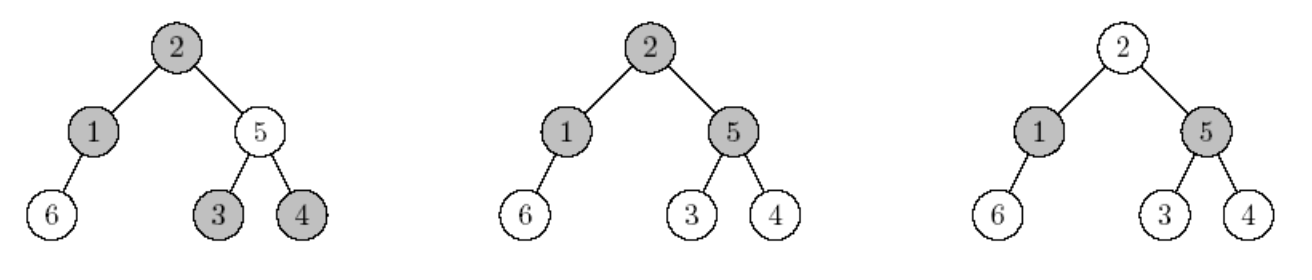
Приклад вхідних даних

6
6 0
1 5
0 0
0 0
3 4
0 0

Приклад вихідних даних

3

Приклад вхідних даних

4
2 0
3 0
4 0
0 0

Приклад вихідних даних

0