Партизанам вдалося визначити всі \(N\) міст на окупованій території, в яких розташовуються ворожі війська, а також \(A_i\) – чисельність ворожих солдатів у \(i\)-му місті.

Відомо, що для перекидання військ німці використовують залізничне сполучення. Було складено детальну карту залізниць, згідно з якою існує рівно \(M\) двосторонніх залізничних колій (доріг). Кожна залізнична колія зв'язує між собою два міста, причому якщо місто \(X\) пов'язане залізницею з містом \(Y\), то, використовуючи цю дорогу, можна дістатися як з міста \(X\) в \(Y\), так і з \(Y\) в \(X\). Будь-яких два міста пов'язує не більше ніж одна Залізна дорога.

Партизанам добре відома німецька прагматичність, згідно з якою для будь-яких двох міст \(S\) і \(F\) (\(1 ≤ S, F ≤ N\), \(S ≠ F\)) існує рівно один шлях (маршрут), що зв'язує міста \(S\) та \(F\). Тобто існує рівно одна послідовність цілих чисел \(P_1, P_2, … P_K\) (можливо порожня), така, що між \(S\) і \(P_1\) є залізниця, між \(P_K\) та \(F\) є залізниця, а також для будь-якого \(i\) від 1 до \(K – 1\) існує залізниця, що зв'язує міста \(P_i\) та \(P_{i+1}\).

Партизани мають два вибухові пристрої, які вони хочуть використовувати для підриву двох залізниць, щоб запобігти швидкому перекиданню ворожих військ у вогнище наступу. Партизанам невідоме місто, з якого почнеться наступ, тому вони хочуть обрати такі дві залізниці, щоб у результаті вибуху максимальне значення військового потенціалу всіх регіонів, що утворилися після вибуху, було мінімальним. Регіоном називатимемо таку максимальну за включенням множину міст, що для будь-яких двох міст з цієї множини існує маршрут, який їх зв'язує. Військовим потенціалом регіону називатимемо суму \(A_i\) для всіх міст, що входять до цього регіону.

Спочатку всі \(N\) міст утворюють один регіон.

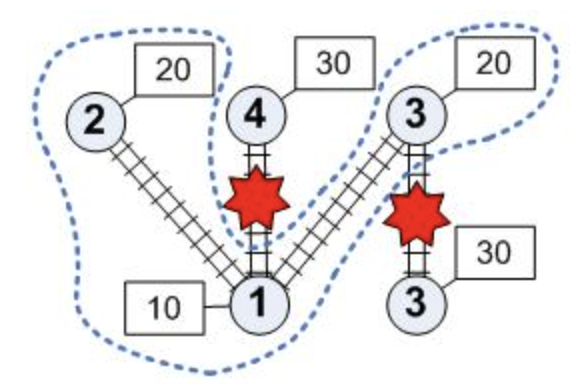
Ваше завдання – допомогти партизанам визначити такі дві залізниці, підірвавши які максимальне значення військового потенціалу регіонів, що вийшли в результаті вибуху, було мінімальним.

Формат вхідних даних

Перший рядок містить два цілих числа \(N\) (\(3 ≤ N ≤ 100 000\)) та \(M\) (\(2 ≤ M ≤ 1000 000\)) відповідно.

Другий рядок містить рівно \(N\) цілих чисел \(A_i\) (\(1 ≤ A_i ≤ 10^9\), \(∑A_i ≤ 10^9\)) – кількість ворожих солдатів у місті \(i\), числа розділені одиночними пробілами.

Наступні \(M\) рядків описують залізниці між містами. Кожен рядок містить два цілих числа \(X_i\) та \(Y_i\) (\(1 ≤ X_i, Y_i ≤ N\), \(X_i ≠ Y_i\)), розділених пропуском, де \(X_i\) та \(Y_i\) – це номери міст, пов'язаних залізницею.

Формат вихідних даних

Перший і єдиний рядок повинен містити два числа – номери залізниць, підірвавши які максимальне значення військового потенціалу регіонів, що утворяться після вибухів, буде мінімальним.

Дороги нумеруються послідовно від 1 до \(M\) у порядку їхнього введення. Якщо є кілька рішень, то виведіть будь-яке з них. Порядок виведення номерів доріг не має значення.

Приклад вхідних даних

4 3
1 1 2 2
2 4
1 2 
3 1

Приклад вихідних даних

3 1

Приклад вхідних даних

5 4
10 20 20 30 30
1 2
4 1
1 3
3 5

Приклад вихідних даних

2 4