Компонентою реберної двузв'язності графа називається така підмножина вершин, що для будь-яких двох вершин цієї підмножини існує не менше двух шляхів які не перетинаються по ребрам.

Іншими словами дві вершини належать одній компоненті реберної двузв'язсності якщо на шляху між ними немає жодного моста (інакше не вийде зробити два шляхи які будуть іти по різним ребрам).

Фактично прибравши в графі мости - граф розпадеться на компоненти реберної двузв'язності.

Заданий неорієнтований граф. Необхідно виділити в ньому компоненти реберної двузв'язності.

Формат вхідних даних

Перший рядок містить два натуральних числа \(N,M\) - кількість вершин та ребер графа. (\(1 \le N \le 20000\), \(0 \le M \le 200000\)).
Наступні \(M\) рядків містять по два числа - номера вершин які з'єднані ребром.

Формат вихідних даних

В першому рядку виведіть \(K\) - кількість компонент реберної двузв'язності.
В другому рядку виведіть \(N\) чисел від \(1\) до \(K\) - номер компоненти кожної вершини.

Приклад вхідних даних

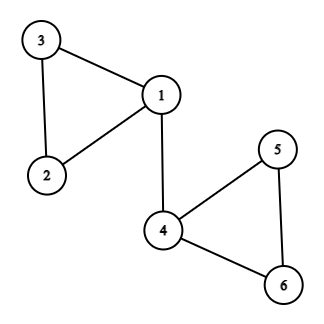
6 7
1 2
2 3
3 1
1 4
4 5
4 6
5 6

Приклад вихідних даних

2
1 1 1 2 2 2