Один із гірськолижних курортів у зв'язку з фінансовою кризою вирішив розширити спектр послуг, пропонуючи траси для катання не лише на лижах та сноубордах, а й на санні траси.

У господарів курорту є топографічна карта території, висоти на якій відображені за допомогою контурів, кожен з яких є коло. У кожному колі вказана висота поверхні, що прилягає до внутрішнього контуру цього кола. Вся територія, яка не знаходиться всередині будь-якого кола, має висоту 0. Оскільки це єдина інформація про місцевість, то можна умовно вважати, що ділянки між колами плоскі. Жодні два кола не перетинаються і не торкаються.

Використовуючи цю карту, необхідно прокласти санну трасу, яка задовольнятиме двом умовам: різниця висот між початковою і кінцевою точками повинна бути максимальна, і кількість контурів, що перетинаються, не повинна перевищувати деякого заданого значення \(𝐾\) (це пов'язано з тим, що те місце, яким сидять на санках, має обмежену міцність). При цьому траса може мати ділянки підйому, але не повинна включати в себе жодної точки, яка була б вище за початкову (туди санки просто не заїдуть).

На наведеному малюнку пунктирною лінією показана найкраща траса для \(𝐾\) = 4. Різниця висот у ній становить 68.

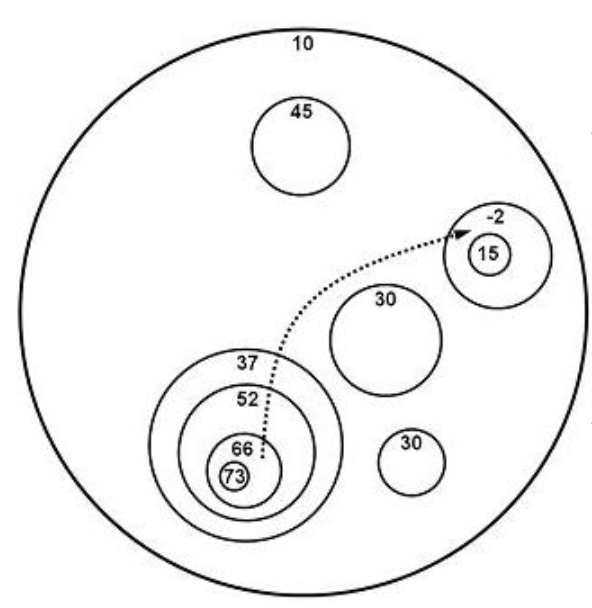
Формат вхідних даних

Спочатку вводяться два натуральні числа максимальна кількість кіл, що може перетнути траса.

Далі йдуть описи кіл, кожне з яких складається з чотирьох цілих чисел: \(X,Y\) (-2000 \le X \le 2000\(, -2000 \le Y \le 2000\) ) - координати центра кола і \(A\) (\(–1000 ≤ 𝐴 ≤ 1000\)) — висота місцевості, що стосується внутрішнього краю кола.

Формат вихідних даних

Виведіть одне число - максимальний перепад висот на трасі.

Приклад вхідних даних

10 4
38 61 2 73
69 34 3 15
61 59 4 30
40 60 5 66
58 44 6 30
71 34 6 -2
47 21 6 45
41 58 8 52
41 57 11 37
48 40 33 10

Приклад вихідних даних

68