Ви є одним із розробників нової комп'ютерної гри. Гра відбувається на прямокутній дошці, що складається з \(W \times H\) клітин. Кожна клітина може або містити або не містити фішку (див. малюнок).

Важливою частиною гри є перевірка того, чи з'єднані дві фішки шляхом, що задовольняє наступні властивості:

• Шлях повинен складатися з відрізків вертикальних і горизонтальних прямих.
• Шлях не повинен перетинати інші фішки.

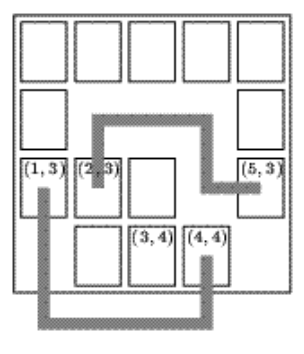
При цьому частина шляху може опинитися поза дошкою. Наприклад:  

Фішки з координатами (1,3) та (4,4) можуть бути з'єднані. Фішки з координатами (2,3) та (5,3) теж можуть бути з'єднані. А ось фішки з координатами (2,3) і (3,4) з'єднати не можна - будь-який шлях, що їх з'єднує, перетинає інші фішки.

Вам необхідно написати програму, яка перевіряє, чи можна з'єднати дві фішки шляхом, що має вищевказані властивості, і, у разі позитивної відповіді, визначальну мінімальну довжину такого шляху (вважається, що шлях має злами, початок і кінець тільки в центрах клітин (або «уявних клітин») », розташованих поза дошкою), а відрізок, що з'єднує центри двох сусідніх клітин, має довжину 1).

Формат вхідних даних

Перший рядок містить два натуральні числа: \(W\) – ширина дошки, \(H\) – висота дошки (\(1≤W,H≤75\)).

Наступні \(H\) рядків містять опис дошки: кожен рядок складається з \(W\) символів: символ «X» позначає фішку, символ «.» (Точка) позначає порожнє місце.

Всі інші рядки містять опис запитів: кожен запит складається з чотирьох натуральних чисел, розділених пробілами – \(X_1, Y_1, X_2, Y_2\), причому \(1≤X_1,X_2≤W\), \(1≤Y_1,Y_2≤H\). Тут (\(X_1, Y_1\)) та (\(X_2, Y_2\)) – координати фішок, які потрібно з'єднати (ліва верхня клітина має координати (1,1)).

Гарантується, що ці координати не збігатимуться (крім останнього запиту; див. далі). Останній рядок містить запит, що складається із чотирьох чисел 0; цей запит обробляти не треба. Кількість запитів не перевищує 20.

Формат вихідних даних

Для кожного запиту необхідно вивести одне ціле число на окремому рядку – довжину найкоротшого шляху, або 0, якщо такого шляху не існує.

Приклад вхідних даних

5 4
XXXXX
X...X
XXX.X
.XXX.
2 3 5 3
1 3 4 4
2 3 3 4
0 0 0 0

Приклад вихідних даних

5
6
0

Приклад вхідних даних

4 4
XXXX
XXXX
XXXX
XXXX
1 1 2 1
2 2 3 2
1 1 3 1
3 4 4 3
2 1 2 4
1 1 2 2
0 0 0 0

Приклад вихідних даних

1
1
4
6
11
0