Зал супермаркету має форму прямокутника розміром \(𝑀 \times 𝑁 \), в якому розставлені вітрини розміром 1 x 1. Сторони вітрин є паралельними стінам супермаркету, а відстані від вітрин до стін – цілі числа. У супермаркет привезли нову супервітрину розміром \(K \times 1\) і вивантажили в одному з кутів супермаркету. Потрібно пересунути її у протилежний кут супермаркету. При цьому її не можна повертати, а можна лише пересувати паралельно до стін супермаркету. Напишіть програму, яка за планом супермаркету допоможе визначити, яку найменшу кількість вітрин потрібно забрати, щоб пересунути супервітрину.

Формат вхідних даних

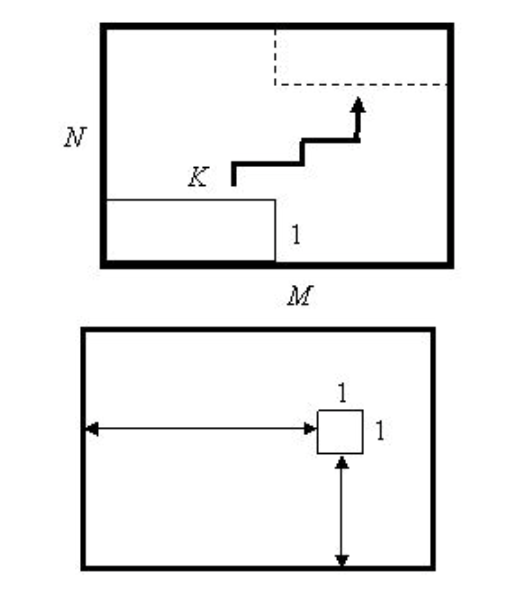
У першому рядку вводяться три натуральні числа \(𝑀 , 𝑁\) і \(𝐾\) (\(𝑀 , 𝑁 ≤ 100\), \(𝐾 ≤ 𝑀\) ). Початкове та кінцеве розташування супервітрини такі, як зазначено на верхньому малюнку.

У наступному рядку записано ціле невід'ємне число \(𝑉\) – кількість вітрин (\(0 ≤ 𝑉 ≤ 𝑁 *𝑀\) ).

У наступних рядках вхідних даних містяться різні пари цілих невід'ємних чисел, що характеризують положення вітрин. Перше число (від 0 до \(M-1\)) - відстань від лівої стіни супермаркету до вітрини, друге (від 0 до \(N-1\)) - відстань від нижньої стіни до вітрини (див. нижній малюнок). Гарантується, що там, де спочатку поставили супервітрину, інших вітрин немає.

Формат вихідних даних

У першому рядку виведіть мінімальну кількість вітрин, які необхідно прибрати.

У другому рядку виведіть можливий маршрут пересування супервітрини: один рядок із великих латинських букв, що позначають наступне:

• U – на 1 вгору,
• D – на 1 вниз,
• L – на 1 вліво,
• R – на 1 вправо.

Кількість символів у рядку не повинна перевищувати \(𝑁 \times 𝑀\). Якщо можливих маршрутів кілька, виведіть будь-який з них.

Приклад вхідних даних

10 10 5
0

Приклад вихідних даних

0
RUURUURUURUURU

Приклад вхідних даних

9 3 2
4
2 0
5 1
5 2
8 2

Приклад вихідних даних

1
URRRDRRRRUU