Задана таблиця з \(H\) рядків та \(W\) стовпчиків.
Нехай \((i,j)\) позначає клітинку в рядку номер \(i\) зверху, та стовпчику номер \(j\) зліва.

В таблиці є \(N\) клітинок в яких знаходиться стіна (через які не можна проходити).

Знайти скільки є способів потрапити з клітинки \((1,1)\) в клітинку \((H,W)\) якщо за один хід дозволяється рухатись лише на 1 клітинку вправо, або на 1 клітинку донизу.

Гарантується, що клітинки \((1,1)\) та \((H,W)\) не містять стіну.

Формат вхідних даних

В першому рядку три цілих числа \(H,W,N\) (\(2 \le H,W \le 10^5\), \(1 \le N \le 3000\)) В наступних \(N\) рядках по два цілих числа \(Ri,Ci\) - що позначають клітинку \((Ri,Ci)\) в якій знаходиться стіна.

Формат вихідних даних

Виведіть кількість способів за модулем \(10^9+7\)

Приклад вхідних даних-1

3 4 2
2 2
1 4

Приклад вихідних даних-1

3

Пояснення до прикладу-1

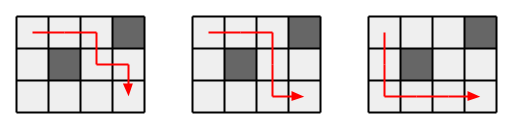
Приклад вхідних даних-2

5 2 2
2 1
4 2

Приклад вихідних даних-2

0

Приклад вхідних даних-3

5 5 4
3 1
3 5
1 3
5 3

Приклад вихідних даних-3

24

Приклад вхідних даних-4

100000 100000 1
50000 50000

Приклад вихідних даних-4

123445622