Дано орієнтований граф з \(N\) вершин, який заданий матрицею суміжності \(NxN\).

Якщо \(Aij=1\) існує орієнтоване ребро з вершини \(i\) в вершину \(j\), а якщо \(Aij=0\) то не існує.

Знайдіть кількість різних шляхів довжиною \(K\) в заданому графі (відповідь виведіть за модулем \(10^9+7\))

Формат вхідних даних

В першому рядку два цілих числа \(N,K\) - кількість вершин графа та довжина шляху(\(1 \le N \le 50\) , \(1 \le K \le 10^{18}\))
В кожному з наступних \(N\) рядків міститься \(N\) цілих чисел \(0\) або \(1\) - матриця суміжності шрафа

Формат вихідних даних

Виведіть кількість шляхів довжиною \(K\) за модулем \(10^9+7\)

Приклад вхідних даних-1

4 2
0 1 0 0
0 0 1 1
0 0 0 1
1 0 0 0

Приклад вихідних даних-1

6

Пояснення до прикладу-1

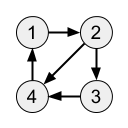
Існує 6 шляхів довжини 2
1 → 2 → 3
1 → 2 → 4
2 → 3 → 4
2 → 4 → 1
3 → 4 → 1
4 → 1 → 2

Приклад вхідних даних-2

3 3
0 1 0
1 0 1
0 0 0

Приклад вихідних даних-2

3

Пояснення до прикладу-2

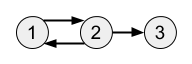
Існує 3 шляхи довжиною 3
1 → 2 → 1 → 2
2 → 1 → 2 → 1
2 → 1 → 2 → 3

Приклад вхідних даних-3

6 2
0 0 0 0 0 0
0 0 1 0 0 0
0 0 0 0 0 0
0 0 0 0 1 0
0 0 0 0 0 1
0 0 0 0 0 0

Приклад вихідних даних-3

1

Пояснення до прикладу-3

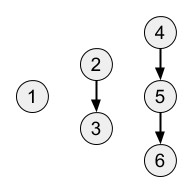
Існує один шлях довжини 3
4 → 5 → 6

Приклад вхідних даних-4

1 1
0

Приклад вихідних даних-4

0

Приклад вхідних даних-5

10 1000000000000000000
0 0 1 1 0 0 0 1 1 0
0 0 0 0 0 1 1 1 0 0
0 1 0 0 0 1 0 1 0 1
1 1 1 0 1 1 0 1 1 0
0 1 1 1 0 1 0 1 1 1
0 0 0 1 0 0 1 0 1 0
0 0 0 1 1 0 0 1 0 1
1 0 0 0 1 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
1 0 1 1 1 0 1 1 1 0

Приклад вихідних даних-5

957538352