Нехай задано дві прямокутні матриці \(A\) та \(B\) розмірності \(M × N\) та \(N × Q\) відповідно:

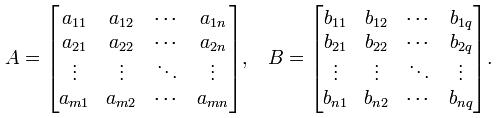
Тоді матриця C розмірності m × q називається їх добутком:

де:

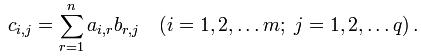
Операція множення двох матриць допустима лише у тому випадку, коли кількість стовбців у першому множнику дорівнює кількості рядків у другому; у цьому випадку кажуть, що форма матриць узгоджена.

Задано дві матриці \(A\) та \(B\). Знайти їх добуток.

Формат вхідних даних

У першому рядку задано два натуральних числа \(na\) та \(ma\) - розмірність матриці \(A\). У наступних na рядках задано по \(ma\) чисел - елемент \(aij\) матриці \(A\).

У (\(na + 2\))-му рядку задано два натуральних числа \(nb\) та \(mb\) - розмірність матриці \(B\). У наступних \(nb\) рядках задано по \(mb\) чисел - елементи \(bij\) матриці \(B\). Розмірність матриць не перевищує 100 × 100, усі елементи матриць цілі числа, які не перевищують за модулем 100.

Формат вихідних даних

У першому рядку вивести розмірність результуючої матриці \(C\): \(nс\) та \(mc\). У наступних \(nс\) рядках вивести через пропуск по \(mc\) чисел - відповідні елементи \(cij\) матриці \(C\). Якщо множити матриці не можна у першому і єдиному рядку вивести число \(-1\).

Приклад вхідних даних-1

2 3
1 3 4
5 -2 3
3 3
1 3 2
2 1 3
0 -1 1

Приклад вихідних даних-1

2 3
7 2 15
1 10 7

Приклад вхідних даних-2

2 3
10 12 31
23 11 17
3 4
0 2 1 4
3 9 2 4
-5 4 2 5

Приклад вихідних даних-2

2 4
-119 252 96 243
-52 213 79 221