Михайло Адріансзон де Рюйтер - найбільш відомий адмірал в історії Данії, добре відомив в англо-датській війні 17 століття, де Рюйтер особисто командував флагманом і давав команди союзним військовим кораблям під час морських битв.

В часи Рюйтера теорія графів лише з'являлась і адмірал використовував всі її переваги при плануванні морських баталій. Шляхові точки в морі відображені вершинами, можливі переходи між ними представлені направленими ребрами. Для будь-яких двох шляхових точок \(W1\) та \(W2\) існує не більше одного прямого переходу. На кожному орієнтованому ребрі записано кількість гарматних ядер, які необхідно вистріляти для безпечного проходу корабля через відповідний перехід.

Одною з найбільш вдалих тактик де Рюйтера був маневр де Рюйтера. Два військових кораблі виходили з однієї точки, розділялись і пробивались крізь ворожий флот, з'єднуючись в пункті призначення. Маневр передбачав рух двох кораблів по двом різним маршрутам, які не перетинаються ні в шляхових точках (крім початкової та кінцевої), ні по жодному з переходів.

Як датчанин, адмірал де Рюйтер не полюбляв витрачати зайві гроші; в морській війні 17 століття це означало використовувати якомога менше дорогих гарматних ядер

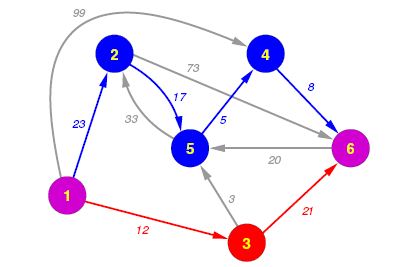
Конкретний приклад тактики де Рюйтера, візуалізований у вигляді графа. Два корабля (червоний і синій) рухаються з спільної початкової точки (1) до спільної кінцевої точки (6). Шлях ченрвоного корабля 1 - 3 - 6 (на шляху потрібно вистріляти 53 ядра); шлях синього корабля 1 - 2 - 5 - 4 - 6 (на шляху необхідно вистріляти 53 ядра). Всього під час маневру необхідно вистріляти 86 ядер. Окрім початкової і кінцевої точки жодна вершина і жодне ребро не відвідані обома кораблями.

Формат вхідних даних

В першому рядку два цілих числа \(N,M\) - кількість шляхових точок та переходів (\(3 \le N \le 1000\)) , (\(3 \le M \le 10000\)).

Кожен з наступних \(M\) рядків містить по 3 цілих числа: \(V1,V2,C\) - початкова та кінцева точки переходу, та кількість ядер які необхідно вистріляти під час цього переходу. (\(V1 \ne V2\)) , (\(1 \le C \le 100\))

Початкова точка руху 1, кінцева точка руху \(N\). Гарантується, що завжди існує не менше двох різних шляхів між точками 1 та \(N\)

Формат вихідних даних

Виведіть найменшу кількість ядер, яку необхідно використати, щоб обидва кораблі дістались кінцевої точки маневру.

Приклад вхідних даних

6 11
1 2 23
1 3 12
1 4 99
2 5 17
2 6 73
3 5 3
3 6 21
4 6 8
5 2 33
5 4 5
6 5 20

Приклад вихідних даних

86