Телекомунікаційна мережа великої IT-компанії містить серверів n, пронумерованих від 1 до n. Деякі пари серверів з'єднані двосторонніми каналами зв'язку, всього в мережі m каналів. Гарантується, що мережа серверів влаштована таким чином, що каналами зв'язку можна передавати дані з будь-якого сервера на інший сервер, можливо з використанням одного або декількох проміжних серверів.

Множина серверів \(A\) називається стійким до відмови, якщо при недоступності будь-якого каналу зв'язку виконано таку умову. Для будь-якого сервера \(X\), що не входить до цієї множини, існує спосіб передати дані по інших каналах на сервер \(X\) хоча б від одного сервера з множини \(A\).

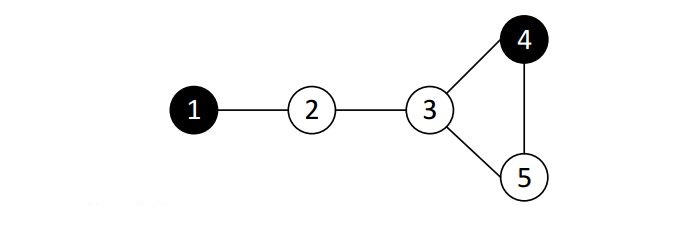
На рис. 1 показаний приклад мережі та стійкості до відмови з серверів з номерами 1 і 4. Дані на сервер 2 можна передати наступним чином. При недоступності каналу між серверами 1 і 2 з сервера 4, при недоступності каналу між серверами 2 і 3 з сервера 1. На сервери 3 і 5 при недоступності будь-якого каналу зв'язку можна по інших каналах передати дані з сервера 4.

У рамках проекту групі розробників компанії необхідно розмістити свої дані у мережі. Для підвищення доступності даних та стійкості до аварій розробники хочуть продублювати свої дані, розмістивши їх одночасно на кількох серверах, що утворюють стійкість до відмов. Щоб мінімізувати витрати, необхідно вибрати мінімальну за кількістю серверів стійкість до відмов. Крім того, щоб дізнатися, наскільки гнучко влаштована мережа, необхідно підрахувати кількість способів вибору такої множини, і оскільки ця кількість способів може бути великою, необхідно знайти залишок від поділу цієї кількості способів число \(10^9+7\). Потрібно написати програму, яка за заданим описом мережі визначає наступні числа: \(k\) — мінімальна кількість серверів у відмовостійкій множині серверів, \(c\) — залишок від поділу кількості способів вибору відмовостійкої множини з \(k\) серверів на число \(10^9+7\)

Формат вхідних даних

Перший рядок вхідного потоку містить цілі числа \(n\) і \(m\) — кількість серверів та кількість каналів зв'язку відповідно \((2≤n≤200000, 1≤m≤200000)\).

Наступні \(m\) рядків містять два цілих числа і описують канали зв'язку між серверами. Кожен канал зв'язку задається двома цілими числами: номерами серверів, які з'єднує.

Гарантується, що будь-які два сервери з'єднані безпосередньо не більше ніж одним каналом зв'язку, ніякий канал не з'єднує сервер сам із собою, і для будь-якої пари серверів існує спосіб передачі даних з одного з них на інший, можливо з використанням одного або кількох проміжних серверів.

Формат вихідних даних

Виведіть два цілих числа, розділених пробілом: \(k\) — мінімальна кількість серверів у відмовостійкій множині серверів, \(c\) — кількість способів вибору відмовостійкої множини з \(k\) серверів, взята за модулем \(10^9+7\)

Приклад вхідних даних-1

5 5
1 2
2 3
3 4
3 5
4 5

Приклад вихідних даних-1

2 3

Пояснення до прикладу-1

В наведеному прикладі стійкими до відмови є наступні множини з двох сервері: {1, 3}, {1, 4}, {1, 5}.