Задано дерево. Спочатку корень дерева має номер 1.
Необхідно підтримувати такі операції:

• LCA(a,b) - знайти найменшого спільного предка вершин a,b
  
• CHROOT(u) - змінити корінь дерева, на вершину u
  

Наприклад, в дереві зображеному на малюнку нижче, LCA(8,7) - вершина 3.

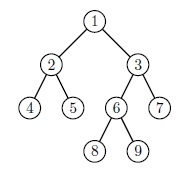
Після операції CHROOT(6) дерево стане таким як на малюнку нижче, і LCA(8,7) - стане вершина 6.

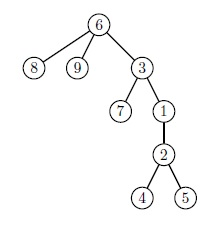
Формат вхідних даних

Вхідні дані складаються з набору тестів.
Перший рядок кожного тесту містить число \(N\) - кількість вершин в дереві.
Кожна з наступних \(N-1\) рядків містить по 2 вершини, що описують ребра дерева.
Наступний рядок містить число \(M\) - кількість операцій.
Кожен з наступних \(M\) рядків містить опис операцій. Рядок "? u v" означає операцію LCA(u,v), а рядок "! u" - операцію CHROOT(u).

Останній рядок містить число 0.

Сума \(N\) для всіх тестів не перевищує 100000. Сума \(M\) по всім тестам не перевищує 200000.

Формат вихідних даних

Для кожної операції "? u v" виведіть її результат в окремому рядку.

Приклад вхідних даних

9
1 2
1 3
2 4
2 5
3 6
3 7
6 8
6 9
10
? 4 5
? 5 6
? 8 7
! 6
? 8 7
? 4 5
? 4 7
? 5 9
! 2
? 4 3
0

Приклад вихідних даних

2
1
3
6
2
3
6
2